Complete Edition USB Memory Stick Samples

Convection and a tea bag

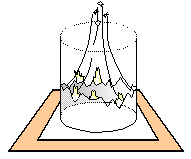
This is a fun experiment to demonstrate convection especially if you use the £10 note!

Take a tea bag, slit one end open and remove the tea. Shape the bag into a cylinder and stand it on a sheet of paper on the bench (a heat resistant mat underneath the paper is not really necessary but might be a good idea the first time you try this). Set light to the top of the bag and wait.

The flame will burn downwards sending a fine stream of ash into the air. As it nears the paper the tea bag continues burning but by this time the upward convection current is sufficient to draw the last remnants of the bag upwards and they simply float away leaving the paper untouched.

Replacing the sheet of paper with a £10 note makes the demonstration even more exciting but if you try it is at your own risk!

Age range: 11-14, 14-16, 16-19, Adult
Apparatus needed: Tea bag Matches Heat resistant mat Sheet of paper £10 note – OPTIONAL!

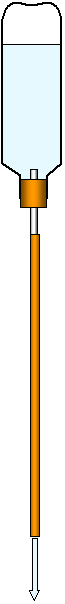
Collapsing bottle and air pressure

This demonstration of atmospheric pressure is very simple and direct and avoids heating cans of air! Completely fill a plastic squash bottle with water - bigger bottles are more impressive. Put a bung in it with a glass tube in the centre and attach a 2 m length of rubber tubing to the tube - more if the height of your lab will allow it. Get someone to hold the end of the tube closed while you climb on a bench and upend the bottle with the rubber tube dangling vertically downwards. Now open the lower end of the tube. As the water runs out the bottle will be squashed flat by the pressure of the air on the outside! The long tube gives a bigger pressure difference between the top and bottom of the water column and also prevents air leaking in.

Theory
Pressure difference between the two ends of the water column of height h = rgh where r is the density of the water.

Age range: 11-13

Apparatus required:
Plastic bottle with rubber tube fitted to a bung in its neck Water Bucket

The wire coat hanger and circular motion

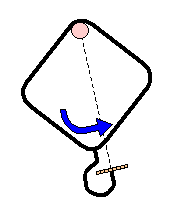
Pull open a wire coat hanger so that it forms a square. File the end of the hook flat and then bend the hook until it points towards the opposite corner of the square. Balance a 1p coin on the hook, put one finger in the corner of the square opposite the hook and then spin the coat hanger in a vertical circle - the coin stays in place! This is a very simple but excellent demonstration of centripetal force.
The force of the hook on the penny always acts towards the centre of rotation. The present record is five 1p pieces stacked on top of each other. With only one penny balanced and with great care I have once even been able to bring the coat hanger to rest without the penny falling off.

Age range: 14- 18

Apparatus required:
Wire coat hanger with filed end Pile of small coins

Mop and back muscles

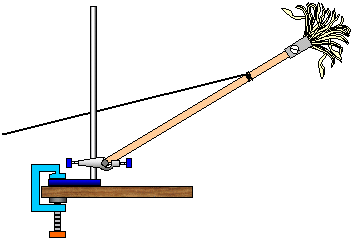
The following demonstration is a simulation of the enormous tension produced in the muscles of your back when you lean over. Tie a piece of string to the handle of a mop about a quarter of the way from the mop head. The head of the mop represents your head and the handle of the mop represents your spine. Drill a hole through the end of the handle furthest from the head and pivot it here, the head of the mop being at the top.

Now try and support the mop as it tilts by holding the string at a small angle to the handle of the mop (I am told that they make an angle of only 10^o with your spine!) The tension in the string represents the huge tension in your back muscles as you bend over. Bending at 45^o produces a tension of over double your own body weight!

Holding something in your hands while you bend over into a car boot will increase the tension even further.

Theory:
The tension in string (back muscles) T is given by the equation:
Tsin A = mg cos q
where A is the angle of the string with the mop (back muscles with the spine) and q is the angle that the mop handle (spine) makes with the horizontal

Age range: 16- 18

Apparatus required:
Mop String Newton meter Metal rod for pivot Retort stand and clamp G clamp

11-14 Sample answers drawn from a number of different files

The questions are shown in black type with the answers in bold blue

1. If you wanted to hang from the ceiling using a rubber sucker how big would it have to be?
(Assume a perfect vacuum in the sucker. Take atmospheric pressure to be 100 000 Pa and use your own weight in Newtons Take g for the Earth as 10 N/kg).
Assume that the weight of the pupil is 500 N. (mass = 50 kg)
Force = Pressure x Area so Area = Force/Pressure = 500/100 000 = 0.005 square metres = 50 square cm.

2. If a second battery is connected in series with the first the current will get …larger…

3. If a smaller current flows through a the lamp the lamp will get …dimmer…….

4. Which planets move fastest in their orbits round the Sun, those close to the Sun or those further away?

……………………those close to the Sun………………………………….

5. Why is this?…………because the gravitational pull of the Sun is greatest there……………….

6. Would it be possible for a given electromagnet to lift a load simply by increasing the current in it? Explain your answer carefully.
Yes up to a point. There will become a time when the iron core will be fully magnetised.

7. If an ice cube that is floating in a glass of water melts the level of water in the glass stays the same. Use that fact to explain why the effect of global warming is more important on the Antarctic ice cap than the Artic ice.
The Arctic ice cap is already floating and if it was to melt the rise in sea level would be quite small. It would actually be zero if the icebergs were floating in pure water and not in salty water. However the Antarctic ice cap is on land and if it melted there would be a considerable rise in the sea level.

8. When white light enters a prism at an angle the red light is bent …less than.. than the blue light.

9. A car accelerates steadily from 15 m/s to 25 m/s in 5 s.
(a) what is the average speed of the car?
(b) what is the acceleration of the car?
(a) Average speed = [25=15]/2 = 40/2 = 20 m/s
(b) Acceleration = change in speed/time = [25 – 15]/5 = 10/5 = 2 m/s²

10. (a) a metal washer is heated. What happens to the hole in the centre of the washer?
(b) What would happen if the piston and cylinder in a car engine were made of metals that expanded by different amounts when heated?
(a) the hole gets bigger – very part of the metal expands but the outer parts of the washer expand more than those nearer the centre
(b) the engine would either seize up or the pistons would become loose in their cylinders

Sample answers (16-19)

The questions are shown in black type with the answers in bold blue. 1. Explain why it is possible for an object travelling in a circle at a constant speed to have an acceleration.
The direction of motion is changing and therefore there is a change in velocity (velocity is a vector) and so there will be an acceleration.

2. A ball mass 2 kg moving left to right at 1.5 ms^-1 collides with a ball of mass 3 kg that is moving from right to left at 0.2 ms^-1. After the collision the 2 kg ball moves from left to right at 1 ms^-1.
Calculate:
(a) the change of momentum of the 2 kg ball
(b) the momentum of the 3 kg ball after the collision
(c) the velocity of the 3 kg ball after the collision
(d) the loss of kinetic energy of the 3 kg ball
(a) Momentum change = m[v – u] = 2[1 - 1.5] = -1 Ns
(b) Momentum of 3 kg ball after collision = -3x0.2 + 1 = 0.4 Ns
(c) Velocity of 3 kg ball = 0.4/3 = 0.13 ms^-1
(d) Loss of kinetic energy of 3kg ball = 0.5x3x0.2² – 0.5x3x0.13² = 0.06 – 0.02535 = 0.035 J

3. A diffraction grating has 300 lines per mm.
Calculate:
(a) the angle of diffraction for the first order image for light of wavelength 550 nm
(b) the highest order possible with this grating at this wavelength
(c) the number of images of the source
Grating spacing (d) = 1/300x10³ = 3.33x10⁶ m
(a) nl = dsinq sin q = 550x10^-9/3.33x10^-6 = 0.165 therefore q = 9.5^o
(b) Highest possible order occurs when the angle of diffraction (q) = 90^o and therefore sin q = sin 90 = 1
n = dsin90/l = 6.06
Therefore the highest order possible = 6 (you cannot have part of an order)
(c) 13 images – six on each side of the centre line and one in the middle

4. A 5 kg mass is hung on a 2.5m length of copper wire of diameter 0.5 mm. If the Young modulus for copper is 1.2x10¹¹ Pa calculate:
(a) the extension produced.
e = FL/EA A = p d²/4 = 1.96x10^-7 m²   Therefore: e = 5.2x10^-3 m = 5.3 mm
(b) the elastic energy stored in the wire Energy = ½ Fe = ½ x 9.8x5x5.2x10^-3 = 0.255J

5. How could the strength of an electromagnet be increased?
Increase current, number and closeness of coils, bend poles closer, introduce an iron core into the electromagnet

6. Describe and explain an experiment to distinguish between the Plum Pudding model of the atom and the Nuclear model.
Rutherford or alpha particle scattering. Fire a beam of alpha particles at a thin sheet of gold foil and observe the scattered alpha particles. The fact that some are deflected through more than 90^o is powerful evidence for the nuclear model of the atom.

Sample lesson plan (11-14)

Refraction at plane surfaces

All teachers may not wish to use all the ideas suggested. It is up to you to fit them to your own pupils’ needs and the school facilities.

For the direct links to material in schoolphysics to work you must be on-line and have subscribed to the premium content.

Pupils should understand how light is refracted at the boundary between two different materials
Introduce the idea of refraction by reference to some everyday phenomena such as:
The apparent depth of a pond or swimming pool
Although not plane refraction it is worth mentioning the bahaviour of lenses and their use in optical instruments (magnifying class, camera, telescope) and the eye (no detail at this point)
Rainbow
The way precious stones flash when light hits them

Refraction is the bending of the light when it enters or leaves a transparent material. Different materials bend light different amounts for the same angle of incidence.

(See: Refraction)

Class experiment
Measure the amount that light refracts when it enters a glass (or Perspex) block. (Probably no mention of refractive index at this level but it could be introduced for a good group who are familiar with the sin function).
Apparent depth of an object when viewed through a block.

(See: Refraction experiments)

Resources needed:
Ray box and electrical supply.
White paper.
Protractor
Glass (or Perspex) block either rectangular or semicircular (see work sheet)

Discus with the pupils that (unlike reflection which occurs in one material) refraction occurs because the light changes speed when it crosses the boundary between two transparent materials – light travels slower in glass or water than it does in air.
Speed of light in air (roughly the same as the speed of light in a vacuum) = 300 000 000 m/s
Speed of light in water = 226 000 000 m/s
Speed of light in glass = 200 000 000 m/s
Speed of light in diamond = 124 000 000 m/s
Show a diagram or animation of a car driving from concrete into sand or a group of soldiers marching from concrete to sand. As the marching soldiers meet the sand at an angle those on one side of the row slow down before those on the other and so the row twists – a useful analogy or refraction.
(See: Refraction and soldiers)

It is the bending of the light that is used by lenses to focus images of an object.

Extension topics:
Total internal reflection
Pupils should do an experiment to investigate total internal reflection and the critical angle.
(See: Total internal reflection)
Mirages
Fibre optics
(See: Fibre optics)

Follow up or homework topics:
Find out about refractive index
Why does a glass test tube disappear when immersed in glycerine?
Draw a diagram showing real and apparent depth and discuss the problem of a fisherman trying to spear a fish.
Old glass in widow panes sometimes distorts because the two sides are not quite parallel. Why is this?

Sample lesson plan (14-16)

Force, work and energy

All teachers may not wish to use all the ideas suggested. It is up to you to fit them to your own pupils’ needs and the school facilities.

For the direct links to material in schoolphysics to work you must be on-line and have subscribed to the premium content.

Pupils should know the quantitative relationship between force and work

Work and energy

The idea of this work is to get the pupils to understand that work is done and energy is converted from one form to another when a force moves through a certain distance. The greater the force and/or the greater the distance the more work is done.
(See: Work)

Class worksheet
Trains – use the sheet headed trains to deduce the relationship between force and work.
This is a most useful resource and should be of great help when introducing this topic.
(See: Trains)
(See: Forces and energy)

The pupils should have understood the formula:

Work done and energy converted = Force x Distance moved in the direction of the force

Pupils should be aware that for an answer for the energy in joules the distance must be measured in metres.

Teaching point:
It may seem rather advanced at this stage to talk about the direction but we can demonstrate that very simply. Get one of the pupils to lift a heavy weight – a large amount of work is done. Now get then to push it along the floor – less work is done. Why?
In the first case they were using force in their muscles to move it against gravity whereas in the second case they only needed to overcome friction.

Follow up work and homework:
Problems involving the formula Work = Force x Distance moved
(See: Work and energy)

Discuss the use of a ramp and other simple machines.
The ramp is a very good example because it does not reduce the work done compared with a straight lift – indeed the energy used will be slightly greater due to frictional forces. What is does do is to reduce the effort by increasing the distance moved.
(See: Machines)

If time allows there are a number of good class experiments involving pulleys that could be done.
(See: Pulleys)

Sample lesson plan (16-19)

Radioactivity

All teachers may not wish to use all the ideas suggested. It is up to you to fit them to your own pupils' needs and to the school's facilities.

For the direct links to schoolphysics material to work you must be on-line and have subscribed to the premium content.

Origins of the background radiation
Discuss the origins of background radiation. Point out that they could go through their lives and not be aware of its existence. Show them a map of the radon concentration around Britain with emphasis on the granite of the South West.
(See: Teachers' CD/oht sheets/nuclear/Background pie chart)
(See: Teachers' CD/oht sheets/nuclear/Background radiation)

Demonstration experiment
Geiger counter in the lab to demonstrate the existence of background radiation.

Discuss with the students the number of 'impacts' per second and the potential 'damage' to the human body. How many 'impacts' have they received during their lifetimes? Why is this not dangerous? Relate to the number per second and stress that it is this which is important. Compare the size of the Geiger tube with that of the human body.

Use the leaflet produced by NRPB showing the radon levels around this country (this also contains the pie chart for background radiation)

It is always a good idea to spend a little time at this point in talking about the safety precautions needed when working with radioactive sources.

(See: Safety precautions when working with radioactivity)

Ionization
This provides a very useful introduction to the topic.

(See: Radioactivity and ions(14-16 text))

Demonstration experiment
Gold leaf electroscope and an alpha source.
Remove the glass front of the electroscope.
Charge a gold leaf electroscope using either a polythene rod or by touching the cap with a lead from an EHT supply.
Put a lighted taper or match close to the raised leaf. The leaf falls due to ionisation in the air. Now repeat the experiment using an alpha source to give conclusive evidence that the alpha particles produce ions in the air.
Resources needed:
Gold leaf electroscope Radium source Tweezers Polythene rod and duster EHT supply Taper or matches Leads

ALL LEADS SHOULD BE FULLY INSULATED AND THE EXPERIMENT SHOULD ONLY BE UNDERTAKEN BY THE TEACHER

Alpha, beta and gamma radiation

Discuss the experiment with a tube of low pressure helium (Rutherford and Royds) to identify the alpha.
Alpha shown to be helium nuclei and so the A-Z form of an alpha particle would be ⁴₂He.
(See: Alpha particles)

Beta shown to be high speed electrons by deflection in electric and magnetic fields.
(See: Beta particles)

Demonstration experiments
Demonstrate a series of experiments to identify some of the properties of alpha, beta and gamma. Range in air, absorption by a variety of materials and magnetic deflection are all that can be simply performed in the school lab.

ALWAYS DISPLAY THE RADIOACTIVITY SAFETY SIGN WHEN CARRYING OUT EXPERIMENTS USING RADIOACTIVE SOURCES.

Build up a table to show the properties of these radiations
(See: Properties of the radiations)

Teaching notes
Pupils may query the origin of the beta particle. Discuss the difficulty of the beta particles being emitted from the nucleus although no electrons exist there. Conversion of a neutron to a proton, an electron and an anti neutrino. (Do we mention the neutrino – probably have to for completeness)
(See: Neutrinos)
(See: Neutrinos (14-16 text))

Gamma and excited states
Point out that the emission of gamma radiation is a way for the nucleus to get rid of excess energy. The transition of nucleons between energy levels within the nucleus gives out energy in a similar way to the transition of electrons between those in the atom.

Inverse square law for gamma radiation
Point out that even in a vacuum the intensity of gamma radiation decreases with the square of the distance from the source in just the same way as light. They are both electromagnetic radiation. Show a diagram to illustrate this.

Exponential law of radioactive decay
Measurement of the 'half life' of water to demonstrate exponential decay.
(See: Teachers' CD/Creative teaching ideas/Radioactive decay)

Analogue experiment with dice or marked wooden blocks.
(See: Teachers' CD/Creative teaching ideas/Radioactive decay)

Discuss the exponential law of radioactive decay starting with dN = - lN
Lead on from this to the law: A = A_oe^-lt It is likely that the specification will not require the law to be proved since it involves integration but if the class can cope it is well worth doing.

Demonstration experiment
Measurement of the half-life of thoron.
(See: Radioactive decay of thoron)

Take suitable care with this experiment – radioactive powder and gas.

Teaching note
The alternative formula for radioactive decay A = A_o/2ⁿ where n is the number of half-lives that have passed is very useful especially for the less mathematically able students. It should be mentioned.

Set problems on radioactive decay
(See: 16-19/Problems/Half life)

Radioactive decay series - decay chains
Mention the radioactive decay series (decay chains).
Show the connection between the relative amounts of different elements in a sample and their half lives.
(See: Radioactive decay chains)

Particle detectors

Discuss the various types of particle detector and then go on to consider the Geiger tube in detail.

Spark counter
Demonstration experiment
Show the students a spark counter detecting alpha radiation. The counters usually available in schools will be unable to give enough ions to detect the passage of beta or gamma.
(See: Spark counter)

Cloud chamber
Show the students both the expansion and diffusion types of cloud chamber. If safety considerations allow let the students investigate the diffusion cloud chambers for themselves.
(See: Cloud chamber)

Bubble chamber
Try and have some bubble chamber photographs available for the students to look at.

Demonstration experiment
Show the students the following experiment to show what happens in a bubble chamber.
(See: Teachers' CD/Creative teaching ideas/Nuclear)

X ray diffraction
Explain the use of X ray diffraction to analyse crystal structure.
(See: X ray diffraction)

Show the students photographs of X ray diffraction patterns formed by materials with differing crystal structure.

Neutron diffraction
Mention the diffraction of other particles such as neutrons.