The work done in the pressure-volume cycle for an ideal gas

We have shown that the work done by an ideal gas which undergoes a change of volume dV at a constant pressure P is P d V.

(a) If the gas changes its volume at a constant pressure, the work done on it is given simply by:

Work done at constant pressure = P(V₂ – V₁)

(b) However if the pressure changes we have to integrate the simple equation to give the total work done for a large volume change.

For n moles of a gas undergoing an isothermal change PV = nRT, and so for a volume change from V₁ to V₂

Work done = integral[PdV] = nRT x integral[dV/V ]

Taking the limits of the integral to be from V₁ to V₂ we have:

Work done at constant pressure = P(V₂ – V₁)

Example problems
(a) An ideal gas with a volume of 0.1 m³ expands at a constant pressure of 1.5x10⁵ Pa to treble its volume.

Calculate the work done by the gas. Work done = 1.5x10⁵x(0.3 - 0.1) = 3x10⁴ J.

(b) Three moles of an ideal gas undergoes an isothermal expansion at 20 ^oC from 0.020 m³ to 0.30 m³. Calculate the work done.

Work done = nRT lg[V₂/V₁] = 3x8.31x293xlg[0.3/0.02] = 8.6 kJ

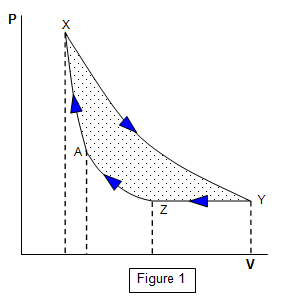
We may represent the work done by a pressure-volume or PV diagram as shown in Figure 1.

Consider a gas at X (volume V and pressure P). Let the gas expand isothermally to Y and then let it be cooled to Z with no change of pressure. It is then compressed isothermally to A and finally compressed adiabatically to X.

The area XYZA enclosed by these PV changes represents the work done BY the gas if the changes take place in the order stated. If the changes take place in the reverse order (XAZY) then the enclosed area is the work done ON the gas.