Measurement of the principal specific heat capacities of a gas

(a) Specific heat capacity at constant volume (c_p)
The specific heat capacity of a gas at constant volume (c_V), can be measured using the differential steam calorimeter invented by Joly in 1886 (Figure 1).

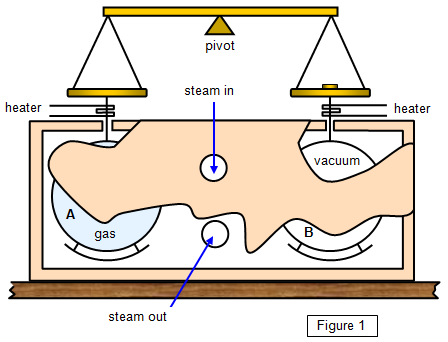
Two hollow copper spheres identical in size and mass are suspended by wire from the two pans of a beam balance. One of the spheres contains a mass of gas M at high pressure (Joly used 22 atmospheres) and the other is evacuated. The spheres are surrounded by a box through which steam is passed.

Steam will condense on the cool spheres, more steam condensing on the one with the greater thermal capacity, that is, the one filled with gas. After some time a mass m has to be placed on pan B to counterbalance the extra mass of steam that has condensed on sphere A.

If c_V is the specific heat capacity of the gas at constant volume and θ_o and q₁ the initial and final temperatures of the sphere, then:

cV = mL/[M(θ₁ -θ_o)]

where L is the specific heat of vaporisation of water.

The two wires are heated to vaporise any liquid condensing on them, and baffles are provided to prevent water dripping off the roof of the box on to the spheres. A control experiment is performed to check the amount of steam condensing on the spheres when both are empty.

(b) Specific heat capacity at constant pressure (c_P)

The specific heat capacity at constant pressure c_P can be measured using the continuous-flow calorimeter devised in 1862 by Regnault. The modern method is a modification of the constant-flow method first used by Swann in 1909.

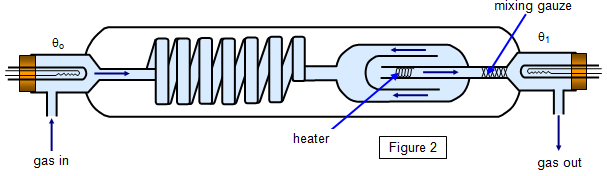
The apparatus is shown in Figure 2. Gas is passed round a series of tubes in a water bath to ensure that it has reached a constant temperature and is then fed into the apparatus at A. Here its temperature is measured using a platinum resistance thermometer (θ_o). It passes over a heater where its temperature is raised, then through a mixing gauze and finally out at B where its temperature is measured again (θ₁).

When steady state has been reached the temperatures are recorded, and hence c_P can be calculated from

VIt = Mc_P(θ₁ – θ_o) + H

where VIt is the energy supplied to the heater in a time t, M is the mass of gas passing through in that time and H is the heat lost. As usual with continuous-flow experiments, by doing two measurements with the same temperature difference but with a different rate of flow H can be eliminated.