The specific heat capacities of gases

For solids and liquids we define the specific heat capacity as the quantity of energy that will raise the temperature of unit mass of the body by 1 K. For gases, however, it is necessary to specify the conditions under which the change of temperature takes place, since a change of temperature will also produce large changes in pressure and volume.

For solids and liquids we can neglect this pressure change and the specific heat capacity that we measure for them is essentially one where the pressure on the body is unaltered. We call this the specific heat capacity at constant pressure (C_P).

The principal specific heat capacities of a gas

The specific heat capacity of a gas will depend on the conditions under which it is measured and since these could vary considerably we will restrict ourselves to the following, called the principal specific heat capacities of a gas:

(a) The specific heat capacity at constant volume (c_v) is defined as the quantity of heat required to raise the temperature of 1 kg of the gas by 1 K if the volume of the gas remains constant.

(b) The specific heat capacity at constant pressure (c_p) is defined as the quantity of heat required to raise the temperature of 1 kg of the gas by 1 K if the pressure of the gas remains constant.

The specific heat capacity at constant pressure (c_p) is always greater than that at constant volume (c_v), since if the volume of the gas increases work must be done by the gas to push back the surroundings.

The molar heat capacity at constant volume (C_V) is the quantity of heat required to raise the temperature of 1 mole of the gas by 1 K if the volume of the gas remains constant. The molar heat capacity at constant pressure (C_P) is the quantity of heat required to raise the temperature of 1 mole of the gas by 1 K if the pressure of the gas remains constant.

The table below gives the principal specific heat capacities for some well-known gases.

Gas	Specific heat capacity at constant pressure (J kg-1K-1)	Specific heat capacity at constant volume (J kg-1K-1)
Air	993	714
Argon	524	314
Carbon dioxide	834	640
Carbon monoxide	1050	748
Helium	5240	3157
Hydrogen	14300	10142
Nitrogen	1040	741
Oxygen	913	652
Water vapour	2020	-

The value of c_P for water vapour is at 373 K.

Connection between C_P and C_V

Imagine a mole of gas enclosed in a cylinder of initial volume V by a frictionless and weightless piston.

The gas is now heated, the volume being kept constant (Figure 1). If the rise in temperature is dT then the heat input is C_VdT, and all this energy goes to raising the internal energy and hence the temperature of the gas; no work is done in expanding the gas.

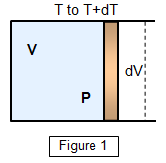
If we now return to the initial conditions and heat the gas again but this time allow it to expand, keeping the pressure constant, the energy input for a temperature rise of dT is C_VdT.

This not only has to raise the temperature of the gas but also must do external work in expanding it by dV. Therefore

C_PdT = C_VdT + dW
C_PdT = C_VdT + PdV

We assume that the gas obeys the ideal gas equation for one mole PV = RT, and therefore PdV = RdT. Substituting for dV we have:

C_P - C_V = R

This formula was first derived in 1842 by Robert Mayer.

The ratio of the two principal specific heats of a gas is denoted by the Greek letter g.

Therefore:

C_P/C_V = γ

The value of this ratio depends on the atomicity of the gas – in other words how many atoms there are in one molecule.