Avogadro's law

This important law was proposed by Avogadro in 1811 and then independently by Ampere in 1814. It states that:

Equal volumes of all gases at the same temperature and pressure contain equal numbers of molecules.

This can be verified using the ideal gas equation. Consider two gases 1 and 2. The gas equation for each gas is:
Gas 1: P₁ V₁ = n₁RT₁ Gas 2: P₂V₂ = n₂RT₂

Now if P₁ = P₂, V₁ = V₂ and T₁ = T₂ we have that n₁ = n₂ and so Avogadro's law is proved.

The volume of one mole of any gas at STP is 22.4 litres. A mole of any substance contains 6.02x10²³ molecules – a number known as Avogadro’s number or Avogadro’s constant (N_A).

Avogadro's constant is the number of particles in a mole of the substance. This number is always the same.
So in:
1 mole of hydrogen (2 g) there are 6.02x10²³ molecules (hydrogen exists as H₂)
1 mole of oxygen (32 g) there are 6.02x10²³ molecules (oxygen exists as O₂)
1 mole of copper (63 g) there are 6.02x10²³ atoms
1 mole of uranium 235 (235 g) there are 6.02x10²³ atoms

For example if we have 2 kg of uranium in a fuel rod we have 2000/235 = 8.51 moles and this contains 8.51x6.02x10²³ = 5.12x10²³ atoms and so 5.12x10²³ uranium nuclei.

Boltzmann's constant (k)

Avogadro's constant is related to another important constant in thermal physics. This is the Boltzmann constant (k) which has a value of 1.38x10^-23 JK^-1.

The Boltzmann constant = R/N_A where R is the universal gas constant (R = 8.31 JK^-1mol^-1).

Dalton's law of partial pressures

If two or more gases are mixed in a container then the final pressure can be found from Dalton's law, which states that:

The pressure in a container is the sum of the partial pressures of the gases that occupy the container.

The partial pressure of a gas is that pressure that the gas would exert if it alone occupied the container.
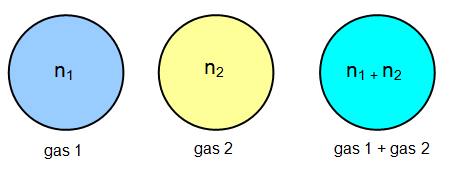
For example, consider a container with a volume V and a temperature T. Let the container be occupied by two different gases, there being n₁ moles of gas 1 and n₂ moles of gas 2. Let the partial pressures of the gases be P₁ and P₂.

Now P₁V = n₁RT and P₂V = n₂RT.
But the total pressure in the container is P, where PV = nRT for n = n₁ + n₂, the total number of moles of whatever type occupying the container.

Therefore: P₁ = n₁RT/V P₂ = n₂RT/ V and P= nRT/V and since n = n₁ + n₂ we have P₁V/RT + P₂V/RT = PV/RT

or

P = P₁ + P₂

which is Dalton's law.


A useful application of this law is in cases where volumes of the same gas occupy separate but connected containers at differing temperatures.

Example problem

A volume of gas V at a temperature T₁ and a pressure p is enclosed in a sphere. It is connected to another sphere of volume V/₂ by a tube and stopcock. The second sphere is initially evacuated and the stopcock is closed.

If the stopcock is opened the temperature of the gas in the second sphere becomes T₂. The first sphere is maintained at a temperature T₁.

Show that the final pressure p’ within the apparatus is: p’ = 2pT₂/[2T₂+T,]

Let there be a molecules of gas, and let there be n₁ molecules in the larger sphere and n₂ molecules in the smaller sphere after the stopcock is opened.

Now n= n₁ + n₂, but pV= nRT. So PV/RT₁ = p’V/RT₁ + p’V/2RT₂
Therefore: p/T₁ = p’(₁/T₁ + 1/2T₂) p’ = 2pT₂/2T₂+T₁