Vibrating strings

If a
string stretched between two points is plucked it vibrates, and a wave travels along the
string. Since the vibrations are from side to side the wave is transverse. The velocity of the
wave along the string can be found as follows.
Velocity of waves along a
stretched string
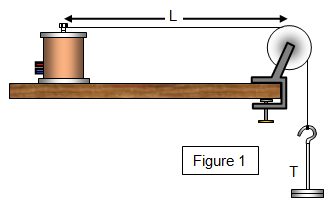
Assume that the velocity of the wave v depends
upon
(a) the tension in the string (T),
(b) the mass of the string (M) and
(c) the
length of the string (L) (see Figure 1).
Therefore: v =
kT
xM
yL
zSolving this gives x = ½ , z = ½ , y = - ½ .
The constant k can be shown to be equal to 1 in this case and we write m as the mass
per unit length where m = M/L. The formula therefore becomes:
velocity of waves on a stretched string = [T/m]1/2
Since velocity = frequency x
wavelength
Frequency of a vibrating string = λ[T/m]1/2
Example problems
1. Calculate the fundamental frequency for a string 0.45 m long, of mass 0.5 gm/metre and a tension of 75 N.
f = 1/2L[T/m]1/2 = 1/0.9x75/[0.5x10-3]1/2 = 430 Hz
2. What is the tension needed to give a note of 1kHz using a string of length 0.5 m and mass 0.75 gm.
Mass/ metre = 1.5x10-3 kg
Tension = f2x4L2xm = 10002x4x0.52x1.5x10-3 = 1500 N = 1.5 kN
The Physics of
vibrating strings
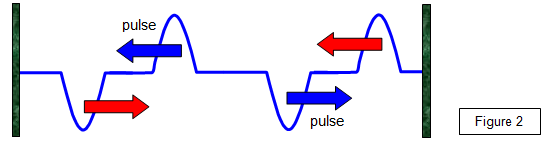
A string is fixed between two points. If the centre of the string is plucked
vibrations move out in opposite directions along the string. This causes a transverse wave to
travel along the string. The pulses travel outwards along the string and when they reaches
each end of the string they are reflected (see Figure 2).
The two travelling waves then interfere with
each other to produce a standing wave in the string. In the fundamental mode of vibration
there are points of no vibration or nodes at each end of the string and a point of maximum
vibration or antinode at the centre.
Notice that there is a phase change when the
pulse reflects at each end of the string.
The first three harmonics for a vibrating
string are shown in the following diagrams.
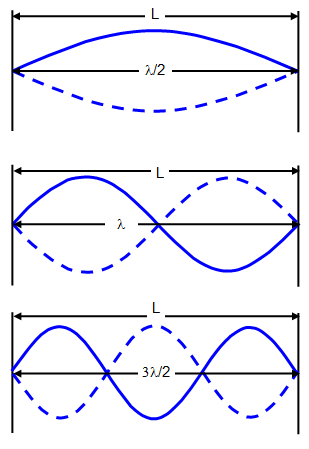
(a) As has already been shown; for a string of length L and mass per
unit length m under a tension T the fundamental frequency is given by:
Frequency (f) = 1/2L[T/m]1/2
(b) First
overtone or second harmonic:
Frequency (f) = 1/L[T/m]1/2
(c) Second overtone or third harmonic:
Frequency (f) = 3/2L[T/m]1/2
A string can be made
to vibrate in a selected harmonic by plucking it at one point (the antinode) to give a large
initial amplitude and touching it at another (the node) to prevent vibration at that
point.

schoolphysics: Waves on strings animation
To see an animation of standing waves on a stretched string please click on the animation link.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB