
This part of the Physics of sound is the basis of all wind instruments, from the piccolo to the organ. Basically the ideas are very simple but they can become complex for a specific musical instrument. For that reason we will confine ourselves to a general treatment of the production of a note from a uniform tube.
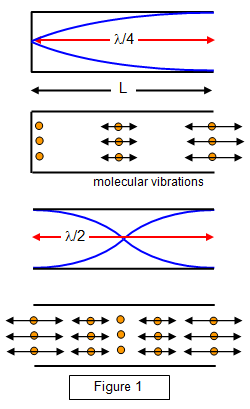
The stationary waves set up by
the vibrations of the air molecules within the tube are due to the sum of two travelling waves
moving down the tube in opposite directions. One of these is the initial wave and the other
its reflection from the end of the tube.
All air-filled tubes have a resonant frequency
and if the air inside them can be made to oscillate they will give out a note at this frequency.
This is known as the fundamental frequency or first harmonic.
Higher harmonics or
overtones may also be obtained and it is the presence of these harmonics that gives each
instrument its individual quality. A note played on a flute will be quite unlike one of exactly
the same pitch played on a bassoon!
A harmonic is a note whose frequency is an
integral multiple of the particular tube's or string's fundamental frequency.
Tubes in
musical instruments are of two types:
(a) open at both ends, or
(b) open at one end
and closed at the other.
The vibration of the air columns of these types of tube in
their fundamental mode are shown in Figure 1. Notice that the tubes have areas of no
vibration or nodes at their closed ends and areas of maximum vibration or antinodes at their
open ends.
An antinode also occurs at the centre of a tube closed at both ends in this
mode.
Nodes are areas where the velocity of the molecules is effectively zero but
where there is a maximum variation in pressure, while the reverse is true for
antinodes.
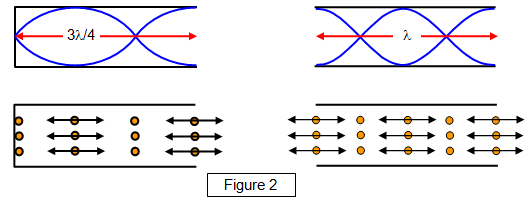
Some of the higher harmonics for the different tubes are shown in Figure
2. Notice that a closed tube gives odd-numbered harmonics only, while the open tube will
give both odd and even-numbered.


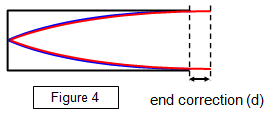
The vibrations within the
tube will be transmitted to the air just outside the tube, and the air will then also vibrate. In
accurate work we must also allow for this effect, by making an end correction (Figure 4).
This means that we consider that the
tube is effectively longer than its measured length by an amount d, that is:
The true
length = L ± d. The equation for a closed tube then becomes:
The velocity of sound in air
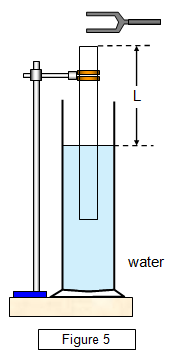
may be found quite simply by using the resonance of a column of air in a tube. An open-
ended tube is placed in a glass cylinder containing water, as shown in Figure 4, so that the
water closes the bottom end of the tube. A tuning fork of known frequency is sounded over
the upper end, the air in the tube vibrates and a note is heard. The length of the air column
is adjusted by raising the tube out of the water until a point is found where resonance occurs
and a loud note is produced. At this point the frequency of the tuning fork is equal to the
resonant frequency of the tube.
In its fundamental mode the wavelength A is four times
the length of the air column (L), that is: l= 4L
Since velocity = frequency x wavelength
the velocity of sound may be found. For accurate determinations the following precautions
should be taken:
(a) the temperature of the air should be taken, since the velocity of
sound is temperature-dependent, and
(b) the end correction should be allowed for. This
may be done by finding the resonance for the second harmonic with the same tuning
fork.