

The picture is of my sons and two friends playing in the Thirsty Nomads heavy metal rock band at Mark’s wedding. The sound was loud – but how load and how does the sound level change as you move further away? Obviously it gets less but how much less?
The level of sound intensity is given in Wm-2 and the comparison between two sounds of intensity I and Io is given in decibels by the formula:
For example using the threshold of hearing as an intensity of 10-12 Wm-2 then we can calculate the decibel level of a sound of intensity 10-6 Wm-2.
Decibel level = 10log(10-6/10-12) = 10log(106) = 60 dB about the intensity at the ears of two people who are having a normal conversation.
However the Thirsty Nomads were probably giving a decibel level of about 100 dB at my ears when I took the photograph. Using the formula we can then work out the intensity of sound at my ears of:
Decibel level = 10log(I/10-12) = 100
Therefore: 1010 = I/10-12 and so I = 1010x10-12 = 10-2 Wm-2.
However the sound intensity will decrease by the inverse square of the distance.
So what about my wife who was a lot further away down the other end of the room? The sound level was obviously less here (to make it simple we will ignore the reflection from the walls of the room).
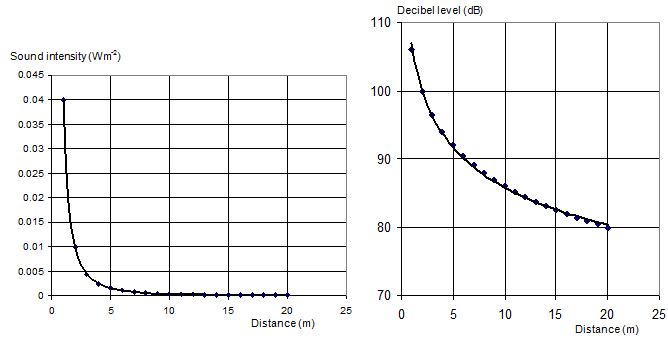
In other words if I was 2m from the group and she was 20 m from it then my wife would have experienced a sound intensity of 10-2x(22/202) = 10-4 Wm-2 (one hundredth of the intensity at my ears) and a decibel level of 10log(10-4/10-12) = 80 dB – still about the noise of a loud stereo sound system!
Doubling the distance between the listener and the sound source will reduce the decibel level by just over 6 dB.
This is calculated as follows:
Intensity is reduced to ¼ of the original and so decibel change = 10log(1/4) = -6.02 dB. The minus sign means a reduction in decibel level. A decrease in distance would lead to an increase in the decibel level giving a plus sign for the decibel change.
The graphs below show the variation of both the sound level intensity and the decibel level with distance from the source of sound taking a decibel level of 80 dB at 20 m.