Elastic energy stored in a stretched wire

When a person jumps up and down on a trampoline it is clear that the bed of the trampoline stores energy when it is in a state of tension. This energy is converted to kinetic and potential energy of the jumper when the tension is removed.

Similarly, when a piece of elastic in a catapult is stretched energy is stored in it, and when the catapult is fired this energy is convened into the kinetic energy of the projectile.

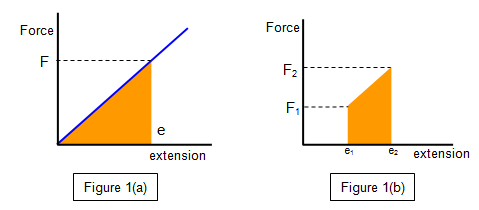
What actually happens within some of the materials mentioned in the examples may be quite complex, but we can calculate the energy stored in a stretched metal wire where Hooke's law is obeyed as follows.

Let the wire be of unstretched length L and let a force F produce an extension e. (Assume that the elastic limit of the wire has not been exceeded and that no energy is lost as heat.)
Consider Figure 1(a). The work done a the force is Fs but in this case the force varies from 0 at the start to F at the end when the wire is stretched by an amount e. Therefore:


But the work done by F is equal to the energy gained by the wire.
Therefore:

work done = average force x extension = ½ Fe

Therefore:


And this energy is the shaded area of the graph.
If the extension is increased from e₁ to e₂ then the extra energy stored is given by:



This is the shaded area on the graph in Figure 1(b), and in general the energy stored in an extension is the area below the line in the force-extension graph. It can also be shown that:

The action of the arrester wire that halts a plane when it lands on the deck of an aircraft carrier is not due to the elastic stretching of the wire. Although as the plane lands the wire does stretch a little virtually all of the plane's kinetic energy is converted to heat energy in a pair of large disc brakes.

However the energy stored in a rubber band can be used to get a very rough idea of the speed of a paper pellet when fired! Air resistance and the heat energy produced in stretched rubber must both be taken into account in this case.

If the wire has been extended beyond the elastic limit and then the force removed the extension is only partially recoverable. Energy is therefore lost due to heat and this phenomenon is known as hysteresis. The force-extension curve for the wire will follow the line OAB on the graph in Figure 2, where the area OABDO is the energy input, OCBD the recoverable energy and the shaded area OABCO represents the energy converted to heat within the specimen. The larger this area the bigger is the energy loss due to hysteresis.

The effect of hysteresis is usually very small for metals, but is noticeable for polythene, glass and rubber. You can easily investigate this using a rubber band. By simply stretching it and then holding it against your lips you can detect a rise in temperature.