The bulk modulus (K)
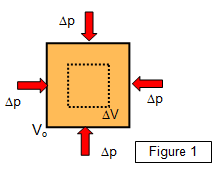
The stress = change in normal
force/area
The strain = change in volume/original volume =
Δp/ΔV
Bulk modulus (K) = - Δp/[ΔV/Vo]
A material is therefore easily
compressed if it has a small bulk modulus. Gases obviously have a much
smaller bulk modulus than solids or liquids. The large bulk modulus for
water explains why a 'belly flop' in diving is so painful!
The
table below shows the bulk moduli for a number of
materials.
| Material |
Bulk modulus (GPa) |
|
Material |
Bulk modulus (GPa) |
| Tungsten |
200 |
|
Steel |
166 |
| Iron (wrought) |
143 |
|
Iron (cast) |
100 |
| Brass |
63 |
|
Copper |
125 |
| Aluminium |
67 |
|
Polystyrene |
5 |
| Rubber |
2.5 |
|
Water |
2 |
| Benzene |
1 |
|
|
|
Student investigation
What are the elastic properties necessary for a good trampoline?
(a) Investigate the relation between the height to which the trampolinist rises and the resulting depression of the trampoline bed.
(b) Investigate the energy storage properties of a catapult by measuring the distance that a given mass may be projected. (Air resistance may be ignored.)
Example problems
The heavy hanging rod (wire)
This is an advanced problem that shows how to deal with a heavy wire that is hanging vertically and where the weight of the wire itself as well as the load produces an extension in the wire.
Force = ke (k is the elastic constant for the wire)
Mass of wire (M) = mass per unit length (m) x length (L)
Tension in the top section length dx = (L-x) mg
Energy = 1/2 [ke] = F/2 x Fe/k = 1/2 [F2e/k]
dE = 1/2 [F2 de/k]
For the whole wire total energy (E) = [m2g2/2k] integral{(L-x)2 dx} = [m2g2/2k]L3/3
But M = mg and so total energy (E) =M2g2/6k
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB
