Focal length and magnification of a spherical surface

Figures 1 and 2 show how light is affected by a single spherical surface of radius R separating two media of refractive indices n₁ and n₂ with n₂ > n₁.


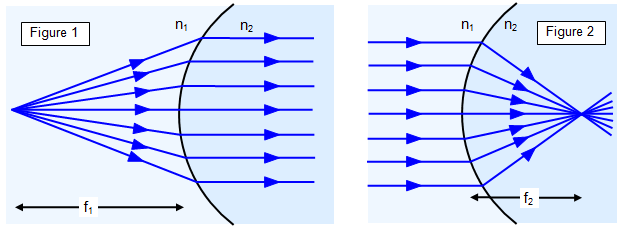
Consider Figure 1:
n₁/u + n₂/v = [n₂ – n₁]/R but if u = f₁ then v = infinity

Therefore:
n₁/f₁ = [n₂ – n₁]/R and so: f₁ = n₁R/[n₂ – n₁]

For Figure 2 u = infinity and v = f₂ giving: f₂ = n₂R/[n₂ – n₁]

Therefore:    f₁/f₂ = n₁/n₂

Magnification

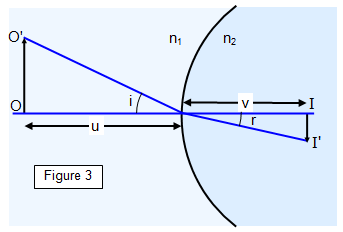
The magnification of the surface can be found using Figure 3.

Consider an object OO' in a medium of refractive index n₁ giving an image II' in medium of refractive index n₂.




II'/v = tan r but this is approximately equal to r for small r and OO'/u = tan i but this is approximately equal to i for small i.

But also n₁i = n₂r and therefore: