Measurement of refractive index

Solids

The refractive index (n) of a solid may be found by:
(a) direct measurement of the angles of incidence and refraction. It can then be calculated from n= sin i/sin r
(b) real depth and apparent depth measurements. It can be calculated from n = real depth/apparent depth
(See: 11- 14/Light/Experiments/Refraction)
(c) using a prism and spectrometer and the minimum deviation method

Liquids

Several methods are available for finding the refractive indices of liquids.
(a) real and apparent depth measurements
(b) the air cell method
(c) the concave mirror method
(d) by a modification of a Newton's rings experiment. This method has the advantage that only a very small amount of liquid is needed
(See: Newton's rings)
(e) Wollaston's method using a right-angled glass block – once again only a small amount of the liquid is required

Gases

The refractive index of a gas is usually found by an interference method.
(See: Interference)

The air cell method
The air cell consists of two glass plates with a narrow air gap between them (Figure 1(a)). This cell is placed in a plane- sided container containing the liquid whose refractive index is to be measured.




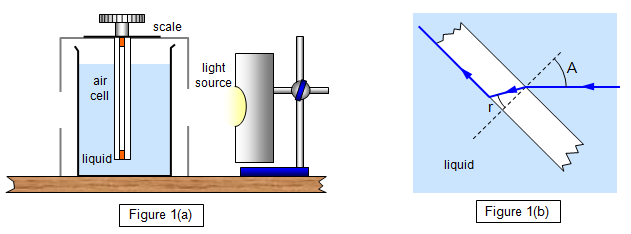
A monochromatic light source is viewed through two slits placed either side of the container, and the air cell rotated until no light passes through the apparatus. A reading is taken of the orientation of the air cell at this position. The air cell is now rotated past the straight-through position until the light is cut out again. The angle of rotation from one position to the other is found (Figure 1(b)).

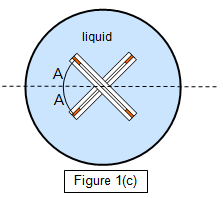
The light does not pass through the air cell because it is totally internally reflected when it travels from the first glass plate towards the air gap. Figure 1(c) shows the conditions that apply when the light is just cut off.
At this point:

n_LsinA = n_gsinr = n_asin90 = n_a and so the refractive index of the liquid is given by:

Refractive index of liquid (n_L) = n_a/sin A = 1/sinA

where A is half the angle through which the air cell is turned between cut-off positions.

Notice that the refractive index of the glass is not required.

The concave mirror method
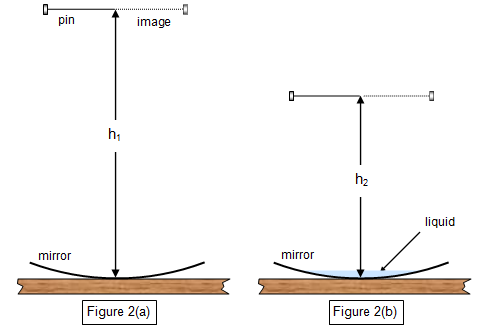
A pin is held vertically above a concave mirror and its position adjusted until there is no parallax between the object and image (Figure 2(a). The distance from the mirror to the pin is then measured (h₁). A small quantity of liquid is placed on the mirror and the procedure repeated giving a new, smaller distance (h₂) (Figure 2(b)).

It can be shown that the refractive index n_L of the liquid is given by

Refractive index of liquid (n_L) = h₁/h₂