
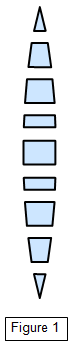
To understand how a lens works we can consider it to be made
up of a number of prisms, each of small angle (Figure 1). If we restrict ourselves to a region
near the principal axis of the lens then the refracting angle of these prisms and hence the
angle of the face of the lens to a beam of parallel light is very small. The central section of
the lens shown in Figure 1 has almost parallel sides.
From the formula for the
deviation of light by a thin prism you can appreciate that as long as we consider only rays
close to the axis and travelling at a small angle to it, then the deviation produced by the lens
is constant and independent of the direction of the ray.
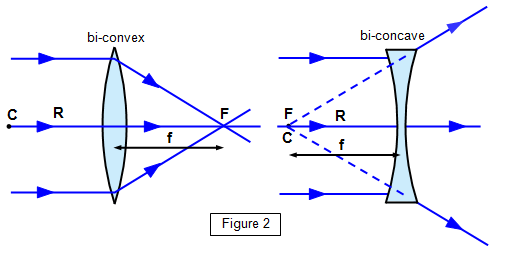
The effect on a beam of
light of a bi-convex lens and bi-concave lens is shown in Figure 2. The principal focus (F),
focal length (f), centre of curvature (C) and radius of curvature (R) are also shown.
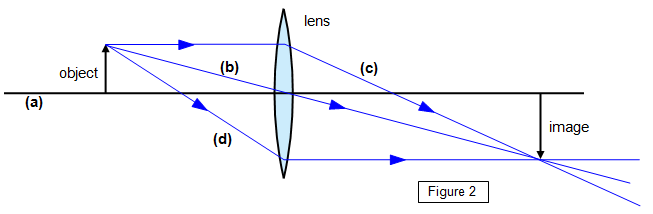
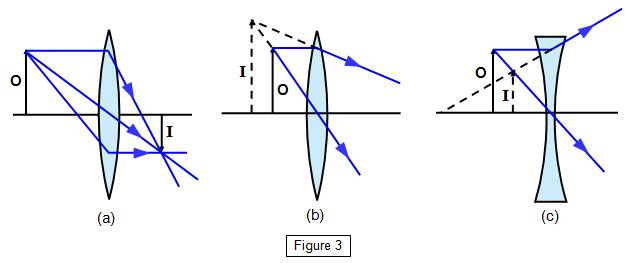
Three lines have to be drawn to represent
respectively
(a) the principal axis,
(b) a ray from the top of the object that passes
undeviated through the centre of the lens (notice that at this point the lens behaves like a
parallel-sided block of glass),
(c) a ray from the top of the object, parallel to the axis that
goes through the principal focus after passing through the lens
An additional line can be
drawn to check the accuracy of the diagram:
(d) a ray from the top of the object through
the principal focus that emerges parallel to the axis.
The image of the top of the object is
at the point where rays b, c and d cross.
The convex lens will give inverted real
images for real objects if u is greater than f and erect virtual images if u is less than f. The virtual images are
always magnified while the real images are magnified if u is between f and 2f. The concave lens will
always give real, erect and diminished images for real objects.
See:
Lenses graphs
Some examples
are also shown in Figure 3.