The lens-maker's formula
The refractive index of the material of the lens a
can be introduced into the lens formula. (Note - we are using the real is positive sign convention here).
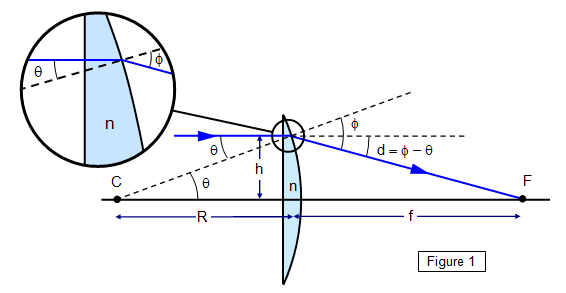
The radius of curvature R = h/θ for small θ, but n = sin φ>/sin θ and therefore n = φ/θ for small angles.
So φ = nθ for small values of θ, that is for rays
close to the principal axis of the lens.
But d = φ - θ. Therefore: (n – 1)θ = h/f and
θ = h/R and so (n – 1)/R = 1/f = 1/u + 1/v
Therefore
for a lens we have:
Lens maker's formula:
n'/f = 1/u + 1/v = (n - 1)(1/R + 1/S)
where R and S are the radii of
curvature of the two faces of the lens, n is the refractive index of the material of the lens and n' the refractive index of the material surrounding the lens (=1 for air). This formula is known as the
lens-maker's formula.
Example problems
1. A lens made of glass of refractive index 1.52 has a focal length of 10 cm in air and 50 cm when completely immersed in a liquid. Calculate the refractive index of the liquid (n').
Using the formula above we have:
(1.52 - 1)2/R = 1/10 and (1.52 - 1)2/R = n'/50
where is the radius of curvature
since R = S.
Therefore R = 10.4, and so 1.104 = 1.52/n' giving n' = 1.38.
2. Calculate the focal length of a glass lens of refractive index 1.5 placed in water of refractive index 1.33, the radii of both surfaces of the lens being 0.10 m.
We have 1.33/f = (1.5 — 1.33)(1/0.1 + 1/0.1)
Therefore: 1.33 = 3.4f
Therefore f = 0.39 m
Compare this with the result for the lens in air, which would be 0.1 m!
See also:
Refraction at spherical surfaces
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB