Radius of curvature and focal length

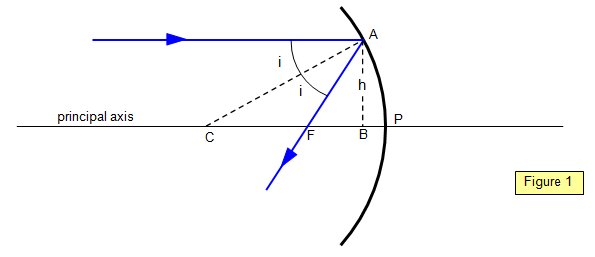
Using the following diagrams we can deduce a simple relationship between the focal length of a spherical mirror and the radius of curvature of the mirror.

The principal focus is marked F and the centre of curvature C. The angle of incidence of the light on the mirror (i) is the same as the angle of reflection (also marked i). The pole of the mirror is marked P. The radius of curvature is CP and the focal length FP.

Figure 1 shows light incident on the mirror far from the principal axis – i.e. the axis that passes through the pole of the mirror.

By trigonometry: CB = AB/tan(i) and FB = AB/tan(2i)
Therefore: CB = FB[tan(2i)/tan(i). In figure 1 i = 32^o and so CB = 3.28xFB

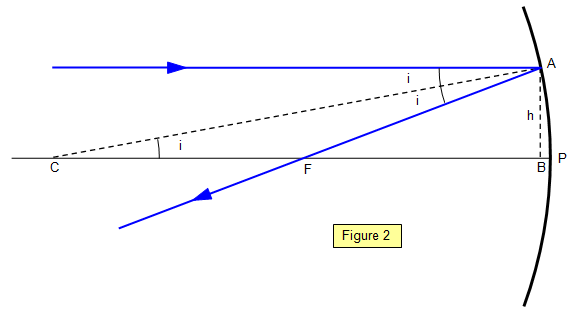
Now look at Figure 2. The ray of light hits the mirror much closer to the pole – therefore much less of the spherical surface is being used for reflection. The length CB is much closer to CP.

Once again: CB = AB/tan(i) and FB = AB/tan(2i)

Therefore: CB = FB[tan(2i)/tan(i). But now i = 12^o and so CB = 2.1xFB. As i tends to zero, in other words as A gets closer to the principal axis, the radius of curvature (CB= CP) becomes closer and closer to twice the focal length (FB=FP). So: