Curved mirrors

There are many different types of curved mirrors but we will consider only spherical and parabolic minors here since they are the most common.

Uses of curved mirrors

Concave mirrors
Reflecting telescopes
Dental mirrors
Headlamp reflectors
Shaving and make up mirrors
Searchlight
Projector
Spherical mirrors and the Cassegrain telescope

Convex mirrors
Safety mirror on dangerous comers
Security mirrors on buses
Anti shoplifting mirrors
Car wing mirrors

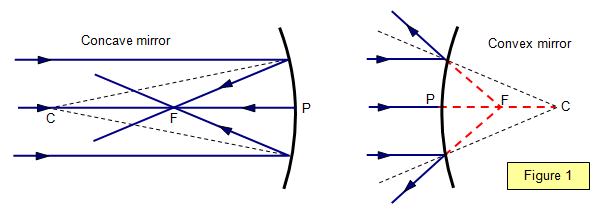
The effects of a concave and a convex surface on a narrow parallel beam of light are shown in the following diagrams.

Some important definitions

The principal axis of a mirror is a line through the centre of the mirror which passes through its centre of curvature
The pole of the mirror is where the principal axis meets the minor
The centre of curvature of a mirror is the centre of curvature of the mirror surface
The radius of curvature of a mirror is the radius of this surface and the distance from the pole of the mirror (P) to the centre of curvature (C).
The principal focus (F) is the point where parallel light close to the axis of the mirror is brought to a focus. The focal length (f) is the distance from the principal focus to the pole of the mirror.

Sign convention

Adopting a sign convention means that we decide to give a positive or a negative value to all measurements of
length.
In this text we will take all real distance as positive and all virtual distances as negative.
Therefore we should point out the following:
(a) for a concave mirror the radius of curvature, the principal focus and the focal length are real
(b) for a convex mirror the radius of curvature, the principal focus and the focal length are virtual

Images in concave and convex spherical mirrors

Let the object distance be u the image distance v and the focal length f. A summary of the results for the image positions for a range of different real object distances in given in the following table.

		Concave			Convex
Object distance		Image type	Image distance		Image type	Image distance
> u >2f		real/inverted	f < v <2f		virtual/erect	f > v > 2f/3
u = 2f		real/inverted	v = 2f		virtual/erect	v = 2f/3
2f > u > f		real/inverted	infinity > v > 2f		virtual/erect	2f/3 > v > f/2
u = f		real/inverted	v = infinity		virtual/erect	v = f/2
f > u > 0		virtual/erect	infinity > v > 0		virtual/erect	f/2 > v > 0
u = infinity		real/inverted	infinity > v > 2f		rvirtual/erect	v = f