
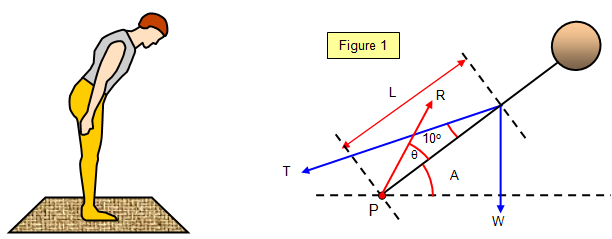
In the section on vectors we looked at the tension in your back muscles when you bend over. One assumption that was made was that the reaction at the pelvis acted long the spine. If this is not so then we need to use the principle of moments to work out the tension in the back muscles.
Let's consider somebody bending over at an angle A to put a heavy case
into the back of a car, probably one of the worst lifting situations.
Let the mass of the
upper body of the person (about 2/3 total body mass) be W, the reaction at the pelvis be R
acting along a line q to the spine (Figure 1) and the load that the
person lifts be mg.
Taking moments about the base of the spine (P) gives:
TL sin 10 = (W + mg) L cos A
You probably know
that the correct way to lift something is by bending your knees and keeping your back straight.
The following calculation shows very clearly why this is! This can be demonstrated very well
by using a mop to represent the spine and a string to represent the back
muscles!
Consider a person bending over so that their spine makes an angle of A with
the horizontal (see Figure 2).
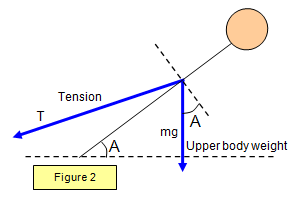
Their
back muscles make an angle of 10o with the spine and have a tension T. We will assume that
the reaction (R) at the pelvis acts along the spine. It has been calculated that the weight of the
upper body (W) is about 2/3 of the total body weight.
Resolving at right angles
to the spine we have: