Simple harmonic motion
Any motion that repeats
itself after a certain period is known as a
periodic motion, and since such a motion can
be represented in terms of sines and cosines it is called a
harmonic motion.
Simple harmonic
motion (s.h.m. for short) is the name given to a particular type of harmonic
vibration. The following are examples of simple harmonic motion:
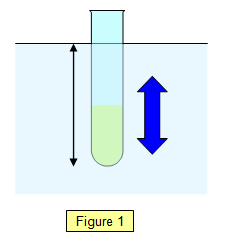
a test-tube bobbing up and down in water (Figure
1)
a simple pendulum
a compound pendulum
a vibrating
spring
atoms vibrating in a crystal lattice
a vibrating cantilever
a trolley fixed
between two springs
a marble on a concave surface
a torsional pendulum
liquid
oscillating in a U-tube
a small magnet suspended over a horseshoe magnet
an inertia
balance
Simple harmonic motion is defined as follows:
A body is undergoing simple harmonic motion if it has an acceleration which is:
(a) directed towards a fixed point, and
(b) proportional to the displacement of the body from that point.
The equations for simple harmonic motion can
be written as follows:
Acceleration (a) = - kx
or dv/dt = - kx
or d2x/dt2 = - kx
where k is a constant and x is the displacement of the body from the fixed point at any
time t.

The maximum
displacement of the body on either side of its central position is called the
amplitude
(r).
The
period of the motion (T) is the time it takes for the body to make one
complete oscillation.
The equation for s.h.m. is usually written as:
acceleration (a) = - ω2x
where ω is a constant (not to be
confused with angular velocity). The value of ω depends on the particular system of
oscillation.
Student investigation
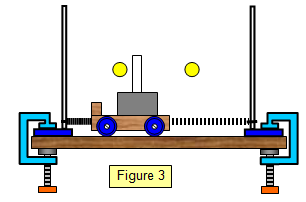
The oscillation of a trolley fixed between two rigid supports by two springs is s.h.m. Using the apparatus shown in Figure 3, find out whether this is true. Using a sensor the variation of displacement and velocity with time may be found. Plot graphs of the values that you obtain. Do they agree with the results that you would expect?

schoolphysics oscillating trolley animation
To see an animation of the motion of a trolley oscillating with simple harmonic motion click on the animation link.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS CD