The helical spring

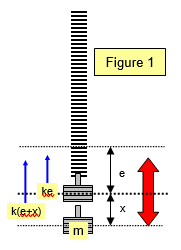
Consider a mass m suspended at rest from a spiral spring and let the extension produced be e. If the spring constant is k we have:

mg = ke

The mass is then pulled down a small distance x and released. The mass will oscillate due to both the effect of the gravitational attraction (mg) and the varying force in the spring (k(e + x)).

At any point distance x from the midpoint:

restoring force = k(e + x) - mg

But F = ma, so ma = - kx and this shows that the acceleration is directly proportional to the displacement, the equation for s.h.m.
The negative sign shows that the acceleration acts in the opposite direction to increasing x.

From the defining equation for s.h.m. (a = -w² x) we have w = k/m = g/e
and therefore the period of the motion T is given by:

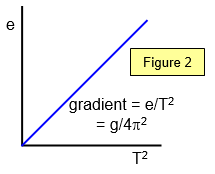
A graph of e against T² can be used to determine g as shown in the diagram.

If the mass of the spring is significant we can allow for it and the corrected equation becomes:

Student investigation
The true equation for an oscillating spring that cannot be considered massless is best investigated using a Slinky spring

Suspend the Slinky so that it has an extended length of about 1 m when hanging freely. Measure the extension (e).

Pull the lower end downwards a little and allow the spring to perform small oscillations in the vertical plane. Record the period of oscillation (T). Repeat the proceŽdure with the spring loaded with a series of small masses.

Plot a graph of T against e² and use it to determine the value of g and the true equation for the spring.

Also plot a graph of the spacing between the spring coils against distance from the top of the spring.

schoolphysics helical spring animation