The floating cylinder
Consider a cylinder of length L and density
r floating in a liquid of density
s. Let the
cylinder have a cross-sectional area A and let a length h be below the surface when the
cylinder is at rest. (See Figure 1)
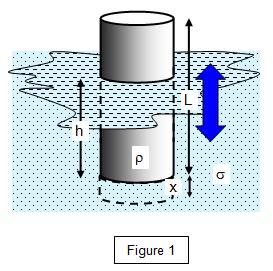
The cylinder is now pushed downwards a little (x) and allowed to
bob up and down, the forces causing the oscillation being gravity and the varying upthrust on
the cylinder.
extra upthrust = extra weight of liquid displaced = A
sgx
therefore restoring force = A
sgx = ma
acceleration (a) = - A
sgx/m = - A
sgx/A
rL = - [
sg/
rL]x
The acceleration is therefore directly proportional to the
displacement (x) and so the cylinder therefore moves with simple harmonic motion.
The
value of
w2 for this system is
sg/
rL
so the period T is:
Period of floating cylinder (T) = 2p/w = 2p(h/g)1/2
since for a floating body the
upthrust = the weight of the body, that is, AL
r= Ah
s.
