
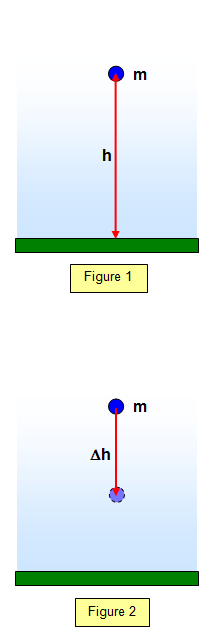
The gravitational potential energy of a mass m is the energy required
to bring the mass m from infinity to a point on the field.
The zero point for the field strength, and therefore for the gravitational energy, being taken as being at infinity.
For this reason gravitational potential energy described in this way is taken as negative.
Energy must be put into an object to raise it away from the surface of the Earth - making its gravitational
potential energy less negative. If this seems strange remember that the input of energy when you lift something is
positive - the change in the gravitational energy of the object is positive.
It can be calculated by simply
multiplying the gravitational potential (VG = g) at the point by the mass m and the vertical distance moved (h) or by using the formula given below based on gravitation theory.
where g is the intensity of the gravitational field (assumed uniform here) and h is the vertical distance moved in the field.
It is important to understand that gravitational energy (= Force x distance) is a scalar.
The energy is converted to other forms when the gravitational potential energy changes due to a movement within the field. (Figure 2) If the distance moved parallel to the gravitational field is Δh then the change in potential energy is:
It is important not to confuse gravitational energy with gravitational potential, the gravitational potential energy refers to a mass m and so the gravitational energy at a point in the field distance r from the centre of the mass producing the field is: