Gravitational intensity below the Earth's surface

Field inside the Earth 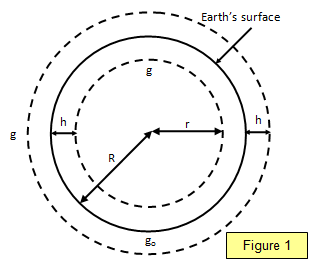Consider a point inside the Earth at distance r from the centre (r< R). Let the field strength at that point be g. Therefore:

g = GM'/2 where M' is the mass of the Earth within radius r. But M' = r³M/R³. Therefore mg = GmMr/R and so:

This means that theoretically the gravitational field intensity decreases linearly inside the Earth; however, this is only true if we assume that the Earth has a uniform density.

In fact the density increases with depth, the density of the Earth's crust being about 2.8x10³ kg m^-3 while that of the surface of the core is 9.7x10³ kg m^-3 .

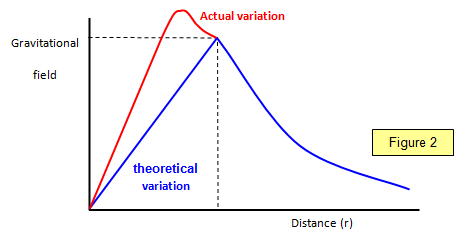
This actually results in an increase in g for a short distance below the surface. The theoretical and actual variations are shown above. If R — r = h, then the theoretical reduction in gravitational intensity at a depth h below the surface is given by:

Gravitational intensity above the Earth's surface

Consider a point a distance r from the centre of the Earth where r > R.

g = GM/r² but g_o = GM/R². Therefore:


For a height h above the Earth's surface, r = R + h. Using the result above, and assuming that h is small compared with the radius of the Earth R, we can say that:



Thus the value of g at a depth h below the Earth's surface is greater than that at the same distance above the surface.