Gravitational Field Intensity (EG)(g)
The gravitational field intensity
(E
G) or (g) is the force on a unit mass at a point in the field.
Since the force (F) on a body of
mass m in a gravitational field of a body of mass M = GMm/r
2 you can see that the
force per unit mass is given by F/m. So:
Gravitational Field Intensity (EG) = (g) = F/m = GM/r2
the units for E
G are Nkg
-1 or since F =
ma, F/m = a and so E
G may be expressed in ms
-2
Uniform field and radial field
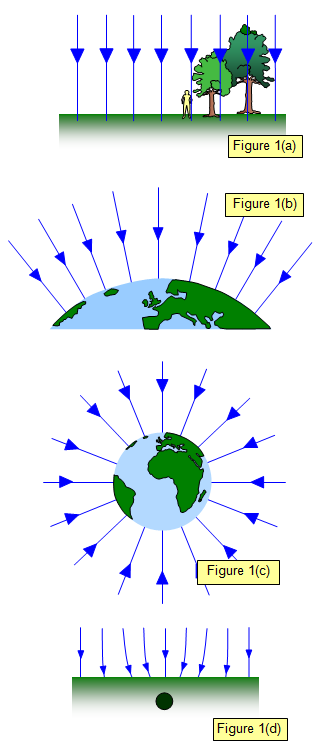
A uniform
gravitational field is one where the field lines are always the same distance apart - this is almost
exactly true close to the Earth's surface (Figure 1(a)).
However if
we move back and look at the planet from a distance the field lines clearly radiate outwards
(Figure 1(b)), getting further apart as the distance from the Earth increases.
When viewed from an even greater distance the complete
field can be seen (as shown in Figure 1(c)).
Such a field is called a radial field - the field intensity
(g) decreasing with distance.
The separation of the field lines gives an indication of the
strength of the field – if they are close together the field intensity is high and of they are far apart it
is low.
Diagram 1(d) shows the distortion of the gravitational field lines by high-
density rock. This was most important for the Apollo Moon landings where NASA discovered
concentrations of massive rock below the lunar surface. The resulting variation in the gravitational
acceleration at that point would have affected the approach of the lunar
lander.
Acceleration of a satellite in orbit and the value of g at that
height
The acceleration of a satellite in orbit is equal to the value of the gravitational field at
that height. Since g can be expressed as either Nkg
-1 or ms
-2
you can see that it can be thought of as an acceleration.
Therefore:
g = GM/r2 = a = v2/r for a satellite moving at velocity v in an orbit of radius r.
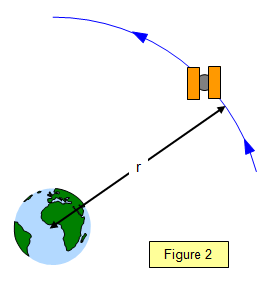
Example problems
A satellite orbits a planet in an orbit or radius 6x106 m where the gravitational field intensity is 0.3 Nkg-1.
(See Figure 2)
Calculate :
(b) the velocity in orbit
(c) the mass of the planet (using G = 6.67x10-11 Nm2kg-2)
(a) centripetal acceleration = g = 0.3 ms-2
(b) velocity in orbit a = v2/r
therefore v = (ar)1/2 = (0.3x6x106)1/2 = 1340 ms-1
(c) Using g = GM/r2 M = gr2/G = 1.6 x 1023 kg
Change in g with height
This is minimal until satellite
orbit heights are reached. In fact for a height of some 200 km above the Earth's surface the g
value has decreased from 9.8 ms-2 to around 7.5 ms-2.
Comparison between
gravitational fields and electric fields
(a) Dependent on BOTH the masses or
charges
(b) Proportional to the inverse square of their separation
(c) Gravitational fields
are ALWAYS attractive
(d) Electric fields can be attractive or repulsive
(e) Electric fields
are affected by the intervening medium
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB