Kinetic energy

The energy possessed by a body by virtue of its motion called the kinetic energy of the body. A rocket traveling to the Moon has kinetic energy as does a snail crawling along a wall. It is the kinetic energy of objects that makes them difficult to stop and the kinetic energy of the air in a hurricane that causes severe damage to the countryside.

The kinetic energy of an object depends on two things:
(a) the mass of the object (m)
(b) its speed (v)

The formula for kinetic energy of an object of mass m travelling at velocity v is:

Proof of the formula for the kinetic energy of an object

Suppose that a body of mass m initially at rest is accelerated by constant force F so that it reaches a velocity v after travelling a distance of s metres. (Figure 1).



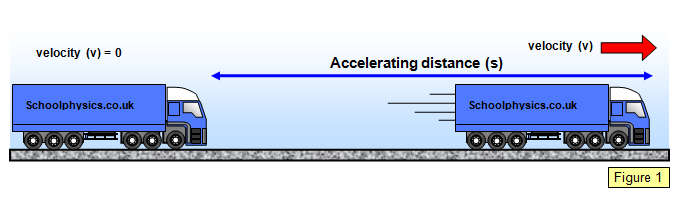
The kinetic energy gained by the body is equal to Fs, and this must therefore be the work done in giving it a velocity v.

However we know that F = ma and v² = u² + 2as where u and v are the initial and final velocities of the object. In this case u = 0 and so we have:

v²= 2as and so ½v² = as

Therefore: kinetic energy = Fs = mas = ½ mv²



The kinetic energy of an object is measured in Joules (J), kilojoules (kJ) or Megajoules (MJ).

Estimate of the kinetic energies of various objects:

speeding car     650 kJ
sprinter          5 kJ
oil tanker      5000 MJ
air molecule      2.5x10^-21 J

Kinetic energy changes

It is important to understand the correct way to calculate changes in the kinetic energy of an object.

For example suppose we want to find the increase in the kinetic energy of an 8kg ball when its velocity is increased from 3 ms^{- 1} to 4 ms^-1. The correct way is as follows:

Kinetic energy increase (Dke) = ½ x8x[4² – 3²] = 4x[16-9] = 4x7= 28 J

and NOT

Kinetic energy increase = ½ x8x[4-3]² = 4 J