Explosions
The conservation of energy and momentum is very
useful in the study of the motion of objects after an explosion. The same ideas can be
applied to firing a rifle, a radium nucleus emitting an alpha particle and a bow firing an
arrow etc.
Kinetic energy in explosions
Consider an explosion, such
as a cannon firing a shell, that produces two fragments of masses m (shell) and M (cannon)
with velocities u and v respectively. (See Figure 1).
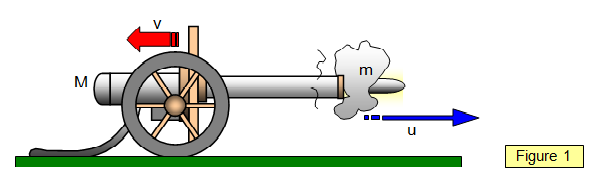
By the law of conservation of momentum the
two objects must move off in opposite directions.
Let the kinetic energy of the shell,
mass m, be E and that of the cannon, mass M, be E'.
Now: E = ½ mu
2 and E' =
½ Mv
2By the conservation of momentum mu = -Mv and
therefore:
E= ½ mu2 and E' = ½ [m2u2]/MThis gives:
Kinetic energy of shell/Kinetic energy of cannon = E/E' = M/m
and so the fragment with
the smaller mass has the larger kinetic energy.
A bullet with a mass one hundredth
that of the gun that fires it will have one hundred times the kinetic energy of the gun.
Example problems
1. A rifle of mass 3 kg fires a bullet of mass 0.025 kg at 100 ms-1. Calculate the kinetic energies of the rifle and bullet.
Kinetic energy of bullet = 0.5x0.025x100x100 = 125
Kinetic energy of rifle = [125 x 0.025]/3 = 1.04J
2. Uranium-235 is an alpha-emitter the resulting nucleus having a mass of 231 units.
If a stationary uranium -235 nucleus emits an alpha particle (mass 4 units) what is the ratio of the kinetic energy of the alpha-particle to that of the residual nucleus?
Kinetic energy of alpha/Kinetic energy of nucleus = E/E' = M/m = 231/4 = 57.75
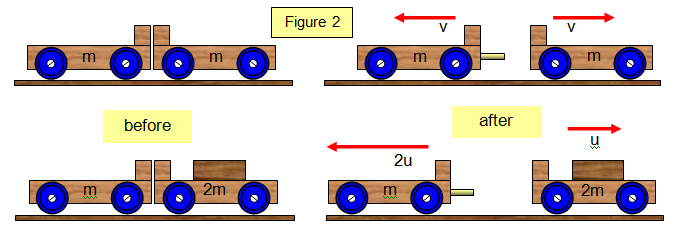
This principle can be
studied with two spring loaded trolleys (Figure 2). If they are put back to back and the spring
in one is released they will explode. Both trolleys move apart with the same speed because
they are of equal mass. In the second diagram trolley 2 moves off with half the speed of
trolley 1 as it has twice the mass.
An interesting case is where no particle is emitted
– e.g. the bow is bulled back under tension and then released with no arrow being fired.
There is a danger of breaking the bow since all the energy stored in the stretched string
goes into the motion of the bow. You can test this by throwing a ball and then doing the
throwing action again but this time without a ball in your hand – it hurts your arm as all the
stored energy must be absorbed by your arm again in bringing it to
rest.
Relative velocity in collisions
It is often very useful to use the
idea of relative velocity in a collision problem. One of the objects involved is considered to be
at rest, the relative velocity of the other is found and then the final velocities of the objects
relative to the frame of reference can be calculated.
The following example
demonstrates the use of relative velocity in a collision problem.
Example problem
A mass m moving to the right with velocity v collides elastically with a mass M moving in the opposite direction also at velocity v (see Figure 3). If M is very much greater than m, calculate:
(a) the velocity of m immediately after the collision
(b) the change in the momentum of in, and
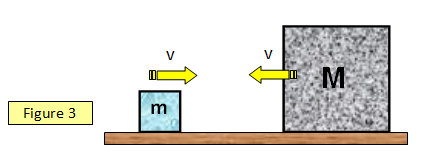
(c) the change in the kinetic energy of m.
(a) Consider M to be at rest; then the velocity of m relative to M is 2v. After the collision the velocity of m relative to M must be –2v, since the collision is perfectly elastic.
Therefore (since M»m) the velocity of M will be virtually unchanged by the collision, and hence the velocity of m relative to the external observer will be (-2v) ± (-v) = -3v.
(b) The momentum change is then mv - m(-3v) = -4mv.
(c) The kinetic energy change is 4mv
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB
