Graphical solutions to equations

We are going to use the vibrating cantilever as an example of the use of log graphs to determine an unknown equation for an experimental arrangement.

The aim of this experiment is to investigate the factors that affect the period of oscillation of a cantilever and also to suggest equations by which they might be related.

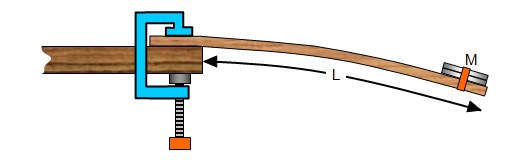
Lets assume that you have done an experiment where you measured the length (L) of the beam, the mass on the end of the beam (M) and the period of oscillation (T). You now want to find an equation that links them but do not know the powers of the three quantities.

We can write an equation as:

T = kM^zL^y

Where k is a constant.

If you now take logs of both sides of the equation we have:

log T = log k + z log M + y log L

Keeping the length of the beam fixed (i.e. L is constant at a known value L_o) means that the equation becomes:

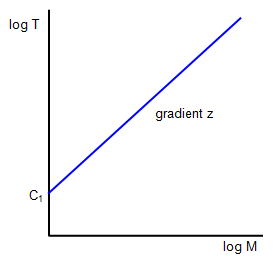
log T = z log M + C₁

where C₁ is a constant (= log k + y log L)

Plotting a graph of log T against log M will give a straight line of gradient z and intercept C₁ as shown in the diagram.

You now have to determine the value of y.

Keeping the mass on the beam fixed (i.e. M is constant at a known value M_o) means that the equation becomes:

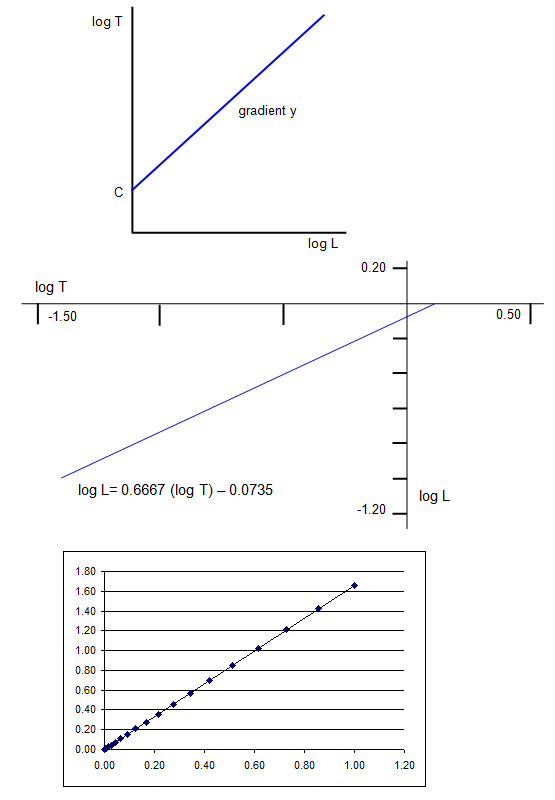
Plotting a graph of log T against log L will give log T = y log L + C₂

where C₂ is a constant (= log k + z log M_o).

(Note that we already know the value of z from graph 1 and so if M_o is known log M_o is also known.)
a straight line of gradient y and intercept C₂ as shown in the diagram.