Drop in current as a capacitor discharges
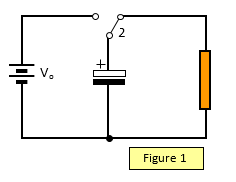
We can use the circuit in Figure 1 to investigate how the current flowing from a capacitor
changes as it discharges.
(We will assume that the capacitor shown has a capacitance of 1000
mF and is discharging through a 10k
W resistor and was charged so that the initial potential difference
across it was 12V).
When it is fully charged the charge on its plates will be Q = CV = 1000x10-6x12 = 12mC.
At the moment the switch is moved to position 2 the initial current flowing from it will be given
by I = V/R = 12.0/10000 = 1.2 mA.
Therefore after 1s 1.2 mC of charge will have flowed from
the capacitor, leaving 10.8 mC on its plates and the potential difference across it will have
dropped to V = 10.8 mC x1000 µF = 10.8V.
The current flowing will now be 1.08 mA (since I = V/R), and after another second the
voltage will be V = 9.72V.
If you repeat the process you can obtain a series of values for the voltage across the
capacitor at any given time.
The time constant
The time that it takes the potential difference across the capacitor to fall to 1/e of its original
value is called the time constant for the circuit. If a capacitor C is discharged through a
resistance R then the time constant is equal to RC. You can see that the time constant is
independent of the initial voltage and this makes it a very useful quantity when using
capacitors in timing circuits.
The time constant (τ) for a capacitor C connected a resistor R = RC
It is important to realise that if the voltage falls to 1/e of the original value in RC seconds then
it will fall to (1/e)/e = 1/e
2 in 2RC s.
You can find out more detail about the use of the time constant in the section showing the
mathematical treatment of charge and discharge.
Example problems
1. What is the time constant for a 4700 μF capacitor discharged through a 1000kΩ resistance?
Time constant = RC = 4700x10-6x1000x103 = 4700 s
2. What will be the voltage across a 100 μF capacitor charged to 20V discharging through a 200kΩ resistor after (a) 20s (b) 40s (c) 2 minutes
For this capacitor – resistor arrangement:
RC = 200x103x100x10-6 = 20 s
(a) time = RC therefore voltage = 20/e = 7.76 V
(b) time = 2xRC therefore voltage = 20/e2 = 2.71 V
(c) time = 6xRC therefore voltage = 20/e6 = 0.05 V
Measurement of the charge stored in a capacitor
The current from a capacitor that is discharging is changing all the time so it is difficult to find
the charge on the capacitor at any given time.
Taking a small interval of time IΔt the charge flowing in that
time is IΔt where I is the average current during that small
time. Therefore if we add together all the little areas made up of the shapes IΔt then we will get the total area under the curve, see Figure 2.
This is of course also the total charge initially present on the charged capacitor.
However since charge = current x time:
The area under the line in an I-t graph = current x time = charge stored
Student investigation
The following readings were obtained from a caacitor discharge experiment. Use them to find the value of the capacitor used.
Voltage across
capacitor (V) |
Time (s) |
Voltage across
capacitor (V) |
Time (s) |
| 12.00 |
0 |
3.85 |
25 |
| 9.56 |
5 |
3.07 |
30 |
| 7.62 |
10 |
2.44 |
35 |
| 6.07 |
15 |
1.55 |
45 |
| 4.83 |
20 |
|
|
Problem
| Time (s) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
| Current (mA) |
15 |
7.3 |
5.4 |
4.6 |
4.3 |
| 4.1 |
Plot a current - time graph from the data above and use it to estimate the charge lost by the capacitor from t = 0 to t = 10s.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS CD
