Mutual inductance

When the current in a coil is changing an e.m.f will be induced in a nearby circuit due to some of the magnetic flux produced by the first circuit linking the second. The phenomenon is known as mutual induction. It is important to realise that the induced e.m.f. lasts only as long as the current in the first circuit is changing.
The mutual inductance M is defined by the equation


where E is the e.m.f induced in the secondary coil and dI/dt the rate of change of current in the primary.
Two coils are said to have a mutual inductance of 1 H if an e.m.f. of 1 V is induced in the secondary when the current in the primary changes at the rate of 1 A s^-1.
Induction coils such as this are used in car ignition circuits, and used to be a source of high voltage for research.


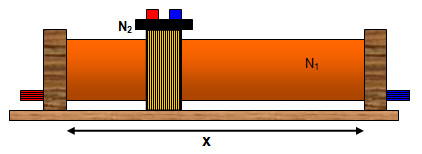
Consider the mutual inductance of a long solenoid and a coil as shown in the diagram.
Suppose that a short coil of N₂ turns is wound round a solenoid of N₁ turns, with a cross-sectional area A, length x and carrying a current I.

The flux at the centre of the solenoid is:     B = m_oN₁I/x

The flux linking the short coil is f = BA and therefore the flux linkage of the short coil is

N₂f =BAN₂= [m_oN₁I/x]AN₂
If the current in the primary changes by dI in time dt, giving a change in flux linkage of d(Nf) in the secondary, then the e.m.f. induced in the secondary will be

E = d(Nf)/dt = [m_oN₁/x]AN₂ dI/dt
Writing M as the mutual inductance, we have that E = - MdI/dt and therefore