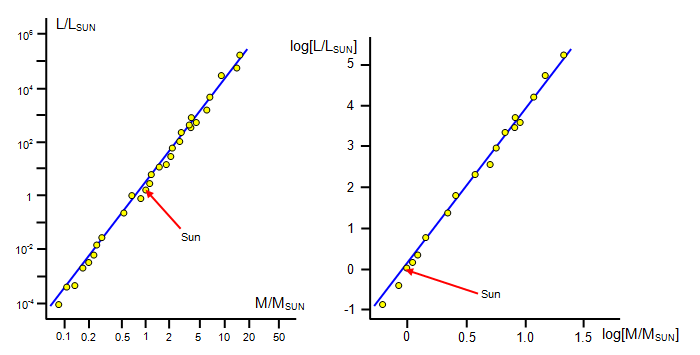

 For stars in the Main Sequence as shown in the Hertzsprung-Russell diagram (and this is about 90% of the stars in our galaxy) there is a fairly simple relationship between the mass of the star and its luminosity.
For stars in the Main Sequence as shown in the Hertzsprung-Russell diagram (and this is about 90% of the stars in our galaxy) there is a fairly simple relationship between the mass of the star and its luminosity. In other words if we compare two main sequence stars and star B has double the mass of star A then the luminosity of star B will be 23.5 = 11.3 times greater than star A. A star of 4 solar masses will have a luminosity nearly 130 times that of our Sun – similar to alpha Leonis (Regulus). Regulus has a surface temperature almost twice that of the Sun and is a little over 77 light years away.
This formula is valid only for main sequence stars, not for white dwarfs, red giants or red supergiants and even for the main sequence the masses must lie between 0.08 and 80 solar masses. For example the red supergiant Betelgeuse has a mass 14 times that of the Sun and using the formula proposed by Eddington the luminosity should be about 10250 times that of the Sun. In fact the average luminosity of Betelgeuse is about 65000 times that of the Sun! (Betelgeuse is a variable star).
One difference between Main Sequence stars and other groups of stars is their density. Main Sequence stars (including our Sun of course) have density around 1600 kgm-3 while the density of a red giant is about 10-4 kgm-3 and that of a red supergiant nearer 10-6 kgm-3.
The graphs below show two ways of presenting the mass-luminosity relation. Figure 1(a) shows luminosity (L/LSUN) plotted against mass (M/MSUN) and Figure 1(b) shows log(L/LSUN) plotted against log(M/MSUN). The gradient of graph (3.5 in this case) gives the power in the mass-luminosity formula.