Hubble's law and the expansion of the Universe.

In 1925 the American astronomer Edwin Hubble (1889-1953) proposed a very simple relationship between the distance of a galaxy and its velocity of recession or approach (v). The Hubble formula provides a very powerful way of determining not only distances of remote galaxies but also the age of the Universe itself.

He stated that they were related by the formula:

where H is Hubble's constant and r is the distance of the galaxy from the Earth. Now clearly the value of Hubble's constant is critical to the measurement of the distance of a given galaxy and therefore to the measurement of the size of the Universe.

At present its value if thought to be about 70 kms^-1 Mpc-¹.

This means that:

The value of H can be found by measuring the distance of another galaxy using the period-luminosity relationship for a Cepheid variable star. The period of intensity variation is directly proportional to the star's absolute brightness. This brightness variation is due to the balance between gravitational attraction and the force due to radiation pressure.

It is important to realise that the number quoted above as the value of H is the value at the present time.

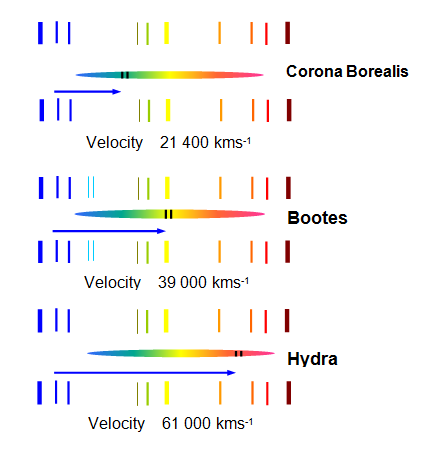
The value of H will have varied over the lifetime of the universe and will continue to do so in the future.


The recession velocity of a given galaxy can be found by measuring the Doppler shift of lines in its spectrum (see Figure 1). Once this is found the distance of the galaxy can be calculated using the Hubble formula.

Value of H in SI units

You can convert the value of H to SI units as follows.
Take the Hubble constant H to be 70 kms^-1 Mpc^-1 and one light year to be 9.46x10¹⁵ m
One Parsec = 3.26 light years = 3.0857x10¹⁶ m therefore 1 Mpc = 3.0857x10²² m
So 70 kms^-1Mpc^-1 = 70x10³/ 3.09x10¹⁶x10⁶ = 2.27 x 10^-18 ms^-1m^{- 1}

Using the result worked out in the previous example we can now calculate the distance of the galaxy in the Virgo cluster.

The radius of the observable Universe

If we take the maximum velocity of recession (v_m) to be that of light (3x10⁸ ms^-1) we can work out the maximum possible radius of the observable universe. (R)
This can be found by using Hubble's formula:
v = HR

R = 3x10⁸x3.09x10²²/70x10³ = 1.33x10²⁶ m

This is equal to 1.4x10¹⁰ light years or fourteen thousand million light years.

The age of the universe

Assume that the radius of the universe (R) = velocity of recession of the most distant galaxies (v) multiplied the age of the universe (t_o) and also that the galaxies have been moving apart with constant velocity since the beginning of time. Written as a formula:

Take R = 1.33x10²⁶ m and if the maximum possible velocity of recession is that of light, the age of the universe (t_o) can be found from the equation

t_o = R/v = 1/H = [1/70x10³] x 3.09 x 10²² = 4.43 x10¹⁷ s = 1.40 x 10¹⁰ years = 14 thousand million years

It seems that Hubble's constant is probably 70 kms^-1 Mpc^-1 with an accuracy of +/- 10%.

Notice that since t_o = 1/H a large value of H implies a young universe.