Distance measurement in Astronomy

The measurement of distance is crucial to our understanding of the scale of the Universe.

Radar

The distance from the Earth of objects in the Solar System can be measured using radar. A pulse is sent out and the time taken for the reflected pulse to be received is recorded. Knowing the speed of electromagnetic radiation in free space and the time between transmission and reception the radar pulse enables us to find the distance of the object. For example the elapsed time would be 2.5 s for the Moon and up to 50 minutes for Jupiter and around five and a half hours for Pluto. (The last two numbers depend on the relative positions of the Earth, Jupiter and Pluto in their orbits)

Parallax

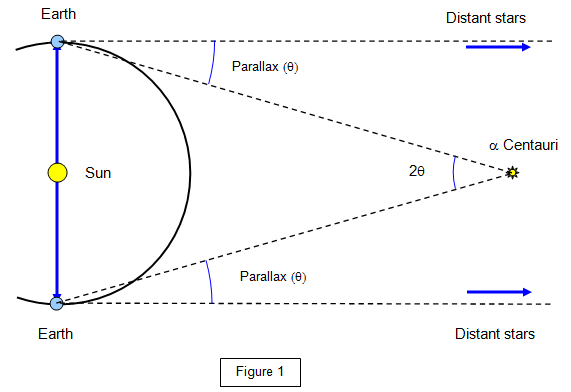
The difference in direction of a star viewed from the two ends of a line with a length equal to the radius of the Earth's orbit is called the PARALLAX of the star.

Stars that are close to the earth clearly have a larger parallax than ones far away. In other words their direction when viewed from the Earth changes significantly as the Earth orbits the Sun.

By significantly we mean a fraction of a second of arc. In the example shown a Centauri (distance 1.33 parsecs) has a parallax of 0.75 " of arc.

schoolphysics parallax animation

To see an animation of parallax click on the animation link.

Astronomical unit

One Astronomical unit (AU) is defined as the mean distance of the Earth from the Sun (1.5x10¹¹ m)

The light year

This is the distance that light travels in free space in one year = 9.5x10¹⁵ m

The Parsec

The radius of Earth's orbit = 1.5x10¹¹ m, and therefore the distance is found from:

tan(1") = 1.5x10¹¹/d so d = 3.06 x10¹⁶ m



Distances between galaxies are usually measured in light years or Mega parsecs (Mpc).



The parallax of a number of stars is shown in the following table.

Star	Parallax (" of arc)	Distance (light years)		Star	Parallax (" of arc)	Distance (light years)
Alpha Centauri	0.750	4.3		Vega	0.133	25
Barnard's star	0.545	6.0		Arcturus	0.097	34
Sirius	0.377	8.6		Aldebaran	0.054	60
Procyon	0.285	11.4		Castor	0.001	570

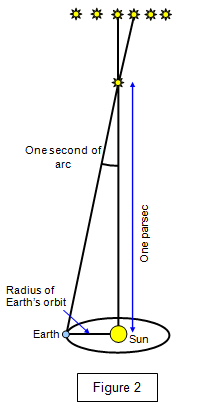
At distances much greater than this the parallax method becomes impossibly difficult to measure. Remember that 1" of arc is the angle subtended by a human head almost ¾ of a kilometer away. Therefore the parallax of Castor is the same as the angle subtended by a human head at a distance of almost 750 km!

Another method for measuring larger distances had to be found.

Cepheid variables

The solution came early in the twentieth century as a result of studies of a variable star (one whose brightness changes with time) in the constellation of Cepheus.

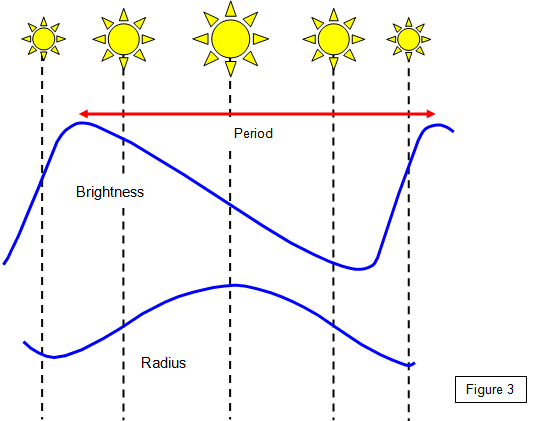
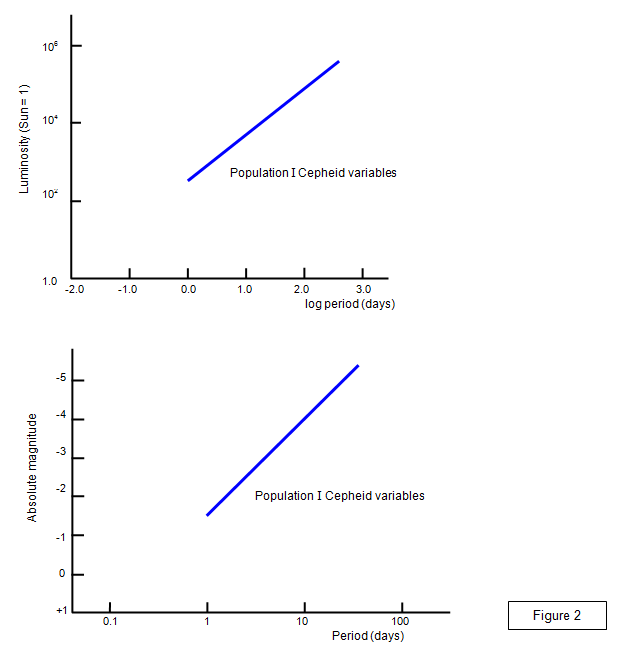
The brightness of the star varied in a particular way (see Figure 3) and in 1912 Miss Henrietta Leavitt of Harvard College observatory discovered an important connection between the period and brightness. This is now known as the period-luminosity relationship. Many other stars were found to vary in a similar way and the group of stars was called Cepheid variables. (There are actually two types of Cepheid variable but we will just consider one type here).


The period- luminosity relation means that if you can measure the period of a Cepheid variable you can find its luminosity. Knowing how bright the star really is and then measuring how bright it appears to be will then give the distance of the star from the Earth. The discovery of Cepheid variables in the Andromeda nebula (M31) enabled its distance from Earth (over two million light years) to be found.

Two ways of presenting the period luminosity law are shown by the graphs in Figure 4.

Of course the period of a variable star in distant galaxies is really difficult to measure and so yet another method was needed to push back the limits of cosmic distance measurement.

The Tully-Fisher relationship

This relationship, named after the two American Astronomers who discovered it, is not yet widely used because of lack of reliable data. It states that the more luminous a galaxy the faster it rotates. Therefore measurement of the rotational speed of galaxies using the Doppler effect gives a way of determining their distance from us.
Astronomers therefore have to turn to the work of Edwin Hubble.