Critical density of the Universe
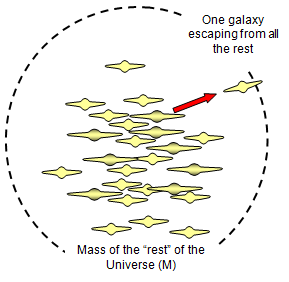
The Hubble constant (H) is important in predicting the ultimate fate of
our universe, related to the concept of its critical density.
The velocity of recession of
a galaxy can be considered as its escape velocity from the rest of the Universe
By
Hubble's formula:
Velocity of recession (v) = HR where R is the distance of the
galaxy.
But the escape velocity is given by the formula:
Escape velocity (v)
= [2GM/R]1/2 so v2 = 2GM/R
where G is the gravitational constant (see Gravitation
section)
Therefore:
v2 = 2GM/R = [2Gr4/3]pR3]/R = 8/3[GrpR2]
But
from the first equation v2= H2R2 and so:
Critical density (r) = 3H2/8pG
[We have assumed both constant v and a
constant value of the Hubble constant (H) in this simplified calculation.]
If the density of
the Universe is greater than this the universe will contract, if it is less it will expand for
ever!
Example problem
Take H = 70 kms-1 Mpc-1 then:
Critical density (r) = 3H2/8pG = [2.27x10-18]2x3/[8x3.14x6.67x10-11] = 9.22x10-27 kgm-3
The mass of a proton is 1.66x10-27 kg so this density is equivalent to just over five protons in every cubic metre of space! (actually 5.56 protons).
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS CD