Analogue and digital signals
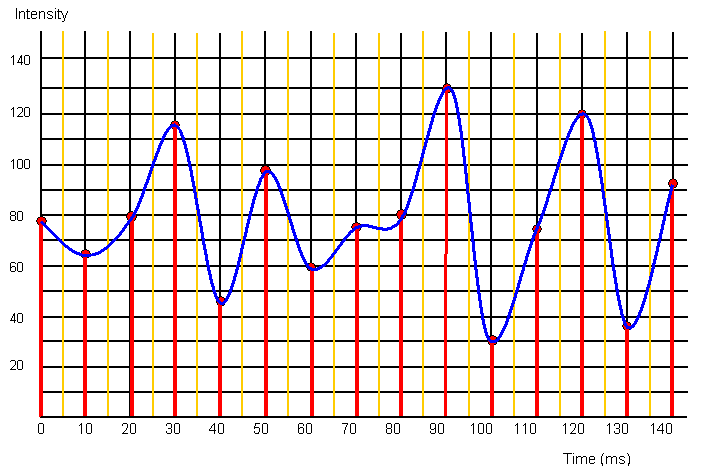
An ANALOGUE SIGNAL is one where
the waveform in the information follows the original waveform exactly at all times
A
DIGITAL SIGNAL is one where the original waveform is sampled at regular intervals and a
number given to the value of the disturbance at each of these points.
Binary
numbers are used for these sampled values.
Binary is a way of expressing numbers
in ones (high voltage value) or zeros (low voltage value) – there is nothing in between. You
can have either a 1 or a 0.
In mathematical language you are expressing numbers to the
base 2 instead of our normal decimal system where we use the base 10.
| Decimal numbers |
Binary equivalent |
|
Decimal numbers |
Binary equivalent |
| 0 |
0000 |
|
8 |
1000 |
| 1 |
0001 |
|
9 |
1001 |
| 2 |
0010 |
|
10 |
1010 |
| 3 |
0011 |
|
11 |
1011 |
| 4 |
0100 |
|
12 |
1100 |
| 5 |
0101 |
|
13 |
1101 |
| 6 |
0110 |
|
14 |
1110 |
| 7 |
0111 |
|
15 |
1111 |
The number of digits in the group gives us the BIT NUMBER. For example all the above
numbers are FOUR BIT NUMBERS. Many of your computers are 32 BIT machines – they
deal with numbers like:
00110011010011100011000110101011
We can
express the following two decimal numbers in eight bit binary :
27 ONE HUNDRED AND TWENTY EIGHT 0 SIXTY FOUR 0 THIRTY TWO 0 SIXTEENS 1
EIGHTS 1 FOURS 0 TWOS 1 ONES 1 = 00011011
53 ONE HUNDRED AND TWENTY EIGHT 0 SIXTY FOUR 0 THIRTY TWO 1 SIXTEENS
1 EIGHTS 0 FOURS 1 TWOS 0 ONES 1 = 00110101
Conversion of analogue to digital - sampling an analogue signal
An example of
the conversion from an analogue to a digital signal is shown below.
The graph shows an analogue signal - the blue line. The value of this signal is 'sampled' at a number of points, in this case 5 ms apart and the value at each of these points is shown in the table.
| Time (ms) |
Signal intensity (decimal) |
Signal intensity (binary) |
|
Time (ms) |
Signal intensity (decimal) |
Signal intensity (binary) |
| 0 |
78 |
01001110 |
|
75 |
56 |
00111000 |
| 5 |
104 |
01101000 |
|
80 |
80 |
01010000 |
| 10 |
65 |
01000001 |
|
85 |
62 |
00111100 |
| 15 |
71 |
01000111 |
|
90 |
130 |
10000010 |
| 20 |
80 |
01010000 |
|
95 |
95 |
01011111 |
| 25 |
35 |
00100011 |
|
100 |
30 |
00011110 |
| 30 |
116 |
01110100 |
|
105 |
62 |
00111110 |
| 35 |
110 |
01101110 |
|
110 |
75 |
00111000 |
| 40 |
46 |
00101110 |
|
115 |
20 |
00010100 |
| 45 |
60 |
00111100 |
|
120 |
120 |
01111000 |
| 50 |
98 |
01100010 |
|
125 |
115 |
01110011 |
| 55 |
72 |
01001000 |
|
130 |
36 |
00100100 |
| 60 |
60 |
00111100 |
|
135 |
83 |
01010011 |
| 65 |
82 |
01010010 |
|
140 |
92 |
01011100 |
| 70 |
82 |
01010010 |
|
|
|
|
The following graph shows only these sampled values with the analogue line removed.
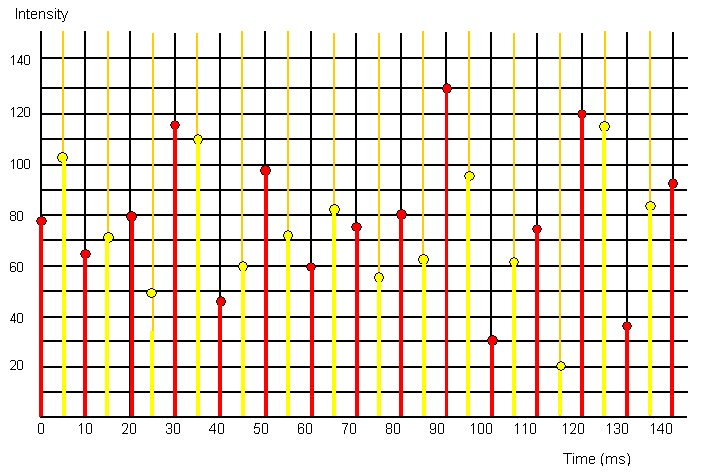
The following three graphs show the problems with sampling. If you only sample at a few times the resulting curve does not really match
the original very well. The red sampled points and the yellow sampled points give different curves from
sampling both the red and yellow points and even this does not quite fit the original wave. Therefore the more
often you sample the wave the better. In a digital CD the original analogue waveform is sampled a staggering 44
100 times a second and for a DVD it can be double this.
The reason for using binary and not ordinary
decimal numbers is to do with interference of the original signal or
noise.
