Weightlessness

We are only really conscious of our own weight because of the reaction of the ground on our bodies. If we removed the ground then there would be no reaction and we would therefore feel weightless. But if there was no ground we would be in a state of free fall, we would accelerate downwards with just the gravitation acceleration at that place. We still do have a weight as there is still a gravitational force acting on us, it is just that we do not feel that weight. In a freely falling lift we would feel weightless until we hit the ground. Astronauts are trained in freely falling aircraft to give them an experience of the weightless conditions in orbit where they are falling freely round the Earth.

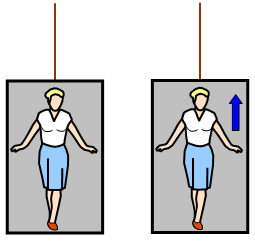
The reverse of this is also true. If we are in a lift that accelerates upwards we feel heavier. This is because we not only feel the reaction of the floor of the lift due to gravitational attraction but there is also an added force - that needed to accelerate us upwards.


The human body cannot tell the difference between 'weight' due to gravitational attraction and that due to acceleration. For this reason scientists have designed space stations that will produce 'artificial gravity' by spinning. The centripetal acceleration produced can be made equal to the gravitational acceleration at the surface of the Earth and so the astronauts feel normal.

Knowing the size of a space station enables you to calculate how fast it would have to spin to give an acceleration of 10 m/s² at its rim.