
I am doing some physics
coursework and cannot find what I'm looking for. My coursework title is "How does the mass
on the end of a spring affect the time period of the spring?" We put different masses on the
end of a spring and then extended the spring an extra 2 cm (to increase the tension
apparently). We then let it go and timed how long 10 oscillations of the spring took, we
divided it by 10 to get the time period of 1 oscillation, we then repeated this with other
masses being put on the end of a spring. I have lots of notes which I just don't understand!
I
would be really grateful for any help you could give me. I cannot seem to find anyone else
who is doing the same coursework either, the coursework needs to be handed in soon too! I
have been trying for a long time to understand it.
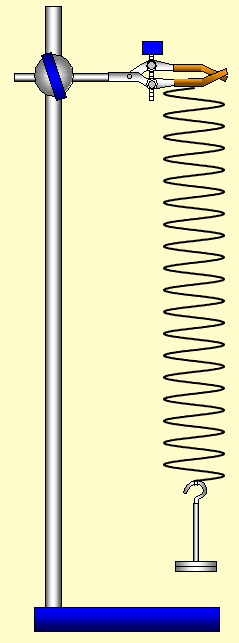
1. Suspend
your spring from a support.
2. Put an initial load on the spring – say 100g
3. Pull the
spring down a little way (about 5 cm although the actual distance does not matter) and then
let go.
4. Time 10 oscillations (you can start at any time but best at either the top or
bottom of an oscillation.
5. Divide by ten to get the time for one oscillation.
6. Add
another 100 g (50g if you can) and repeat the procedure for another five or six masses. You
really need six to get a reliable graph, eight is even better. It is not necessary to pull the mass down
the same distance each time because the period (T) does not depend on the amplitude as
long as the amplitude is not too big.
7. Make a table of the mass and the time for one
oscillation
8. Plot a graph of mass (M) (y axis) against time (T) (x axis)
This should
give you a curve, the T values increasing faster than the M values.
9. Plot a second
graph of (M) (y axis) against T squared (x axis)
This should give you a straight
line.
N.B You must not get the spring to extend beyond its elastic limit. The way to check
this is to make sure that the spring goes back to its original length after each load.
