


Kepler's Laws of planetary motion had stated how the planets
moved in their orbits but they did not explain why. This was left to Sir Isaac Newton, who
was born in Lincolnshire in 1642. Newton was a very gifted man and became Professor of
Mathematics at Trinity College Cambridge at the age of 27! His two most famous
contributions to Physics were Principia, a book on mechanics, and Optiks, a book about
light.
He realised that it was the same type of force that held the Moon in orbit
round the Earth as that which made an apple fall from the tree onto the ground. It was also
the force of gravitational attraction that that held the planets in orbit around the Sun.
Newton's ideas went as follows:
All objects moving in a circle must have a
centripetal acceleration that is directed towards the centre of the circle.
Now we know
the radius of the orbit of the Moon round the Earth and the velocity of the Moon. We can
work out its acceleration towards the centre of the Earth. This turns out to be 0.0027
m/s2
Newton realized that this acceleration must be due to the pull of
gravity of the Earth, but we know that at the Earth's surface the pull of gravity gives all
objects an acceleration of 9.81 m/s2
So clearly the effect of gravity gets
less the further out from Earth we go.
In fact the radius of the Moon's orbit is 60 times
the radius of the Earth and in this distance the gravity has decreased from 9.81 to 0.0027
m/s2. This is 3600 or 60 x 60 times.
Newton used results like the one we
have just seen to work out a formula for the attraction between any two objects. He
assumed that the pull of gravity depended on the masses of both objects and proposed the
following formula for the attraction between two objects of masses, M and m. separated by
a distance d.
Newton's Universal Law of Gravitation has been used to explain some important facts in astronomy such as the tides and the motion of comets. The law also explained why it is that the planets do not follow precise orbits but wobble along their path. This is due to the attraction of other planets. It was the irregular motion of Uranus that led to the discovery of the planet Neptune further out in the solar system.
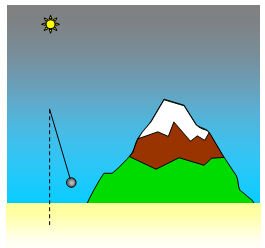
Measurements of the constant of
gravitation (G) are very difficult because of the very small forces involved. Methods have
been devised using mountains and pendulum bobs.
For a more details of these measurements see:
16-19 Gravitational constant measurement
Two mathematical results can
also be deduced from the formula; one is that all bodies that have an inverse square law of
attractive force between them must move about each other in elliptical orbits if they are in
motion.
We can also use the Universal Law of Gravitation and
the formula for the motion in a circle to prove Kepler's Third Law. The law can also be used
to find the masses of the planets or the Sun.