
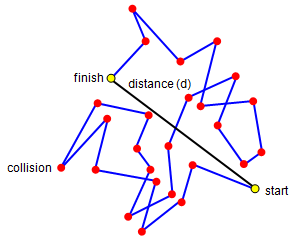
If you look at the work on molecules in a gas you will see that we mentioned a drunk staggering through a crowd! What we would like to know is how far he will have travelled from his starting point after a certain number of collisions. Like the molecule, we will assume that he moves the same distance between collisions, the mean free path. The picture above shows the way he will move for 25 collisions. We can do a simple experiment to work out how far away from the start he will be.
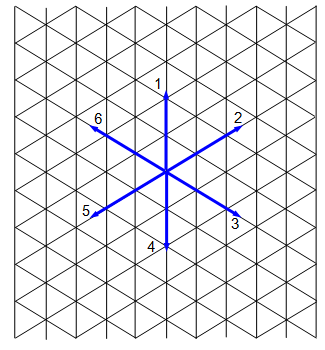
You will need a sheet of special graph paper and a dice. Mark the directions 1 to 6 at one corner of your paper as shown in the diagram. Choose a starting point and throw your dice, mark in a line in the direction shown by the dice. Shake again and mark in a further line, starting where the previous one ended.
Repeat this process for 25 throws. Now measure the distance from the start to the finish in a straight line. (Use the length of one throw as the unit of length.)
You should find that the distance is roughly 5 units.
Repeat the experiment as often as time allows and take the average of the results for the whole
class. The result should now be very close to 5.
It seems as if the distance moved from the start to the finish is the distance between collisions times the square root of the number of collisions (throws).
If you think of doing this with a large number of bromine molecules you should see that we would expect to get a result that was very close to this ideal condition.
Mathematically we can write this as:
Distance (d) = square roof of the number of throws x Mean free path = square roof of N x
Where x is the mean free path and N is the number of throws.
In a liquid, the molecules are very close together although they are in motion and we can consider them to be almost touching each other.
Imagine each molecule occupying a cube with sides of length L where L is just a little more than the diameter of one molecule.
As you know, when a liquid changes to a gas there is a large increase in volume and so the molecules in a gas are much further apart. When water turns to steam, the volume of the steam is 1600 times greater than the volume of the water that produced it. It is this large increase that makes a steam engine work. We can actually measure this increase in volume for liquid air or petrol. In both these cases the volume increase is about 750:1.
Each ‘cube’ occupied by a gaseous air molecule has a volume 750 times greater than that occupied by a liquid air molecule.
We now think back to the bromine diffusion experiment.
You may remember that we measured the distance that the ‘middle brown colour had moved up the tube in 500 s (d).
We took this to be the average distance moved by the bromine molecules in that time.
However, each molecule will have made many collisions in that time and if we ‘straightened out’ the path then each molecule will have travelled a large distance.
We know that the velocity of bromine molecules at room temperature is about 200 m/s and therefore in 500 s the ‘straightened out’ path length is about 100 000 m, and in this distance let’s say that it makes N collisions.
Now if the mean free path is x then 100 000=N x
But we also have the formula:
Distance (d) = square roof of number of throws x Mean free path = square roof of N x
and so substituting for x gives d = 100 000/square roof of N
In the diffusion experiment the distance travelled (d) in 500 s was 0.1 m and this gives
N = 1 000 000 000 000 and a value for the mean free path (x) of 10-7 m 100 nanometres.
To return now to our liquid.
In the liquid the mean free path is much probably less than one molecular diameter
There are 750 times more molecules in a given volume than there were in the gas state.
This means 750 times more chance of a collision. Therefore the mean free path in a liquid be about d/750 or 0.13 nm.
However, we have already said that this will be equal to, or a bit less than, the diameter of an air molecule and so these results mean that an air molecule must have a diameter of somewhere near 0.25 nm.
If you compare this result with the 1.8nm obtained by the oil drop experiment for the length of an oil molecule you will see that - about right. Oil molecules contain more atoms than the oxygen or nitrogen molecules in the air and so you would expect them to be bigger.
The speed of sound depends on the mean free path of the molecules and from the results that you have seen you would expect the velocity of sound to be greater in water than in air and this is the case.
The molecules of water have a smaller distance to move than the air molecules before passing on the sound energy to another molecule by a collision.
You can also see that the velocity of sound increases as the temperature goes up, the molecules are moving faster.
This means a more rapid transfer of sound energy through the air.
Can you suggest why the velocity of so larger in a gas with lighter molecules such helium?