Gravitational attraction and the planets


If
you were to make a journey across our Solar System and land on different planets you would
notice that you weighed different amounts on the different planets. This is because the
gravitational field on their surface is different one from the other.
If the gravitational
field was double that on Earth you would weigh twice as much as you do on Earth – and so
would everything else!
| Planet |
Mass
(Earth = 1000) |
Radius
(km) |
Density
(kg/m3 |
Gravitational field
(N/kg) |
Mass/Radius2
(N/kg) |
| Mercury |
55 |
2440 |
5420 |
3.8 |
9.2 |
| Venus |
812 |
6050 |
5250 |
8.8 |
22.2 |
| Earth |
1000 |
6400 |
5510 |
9.8 |
24.4 |
| Mars |
110 |
3380 |
3960 |
3.8 |
9.6 |
| Jupiter |
317000 |
71400 |
1330 |
25 |
62.2 |
| Saturn |
95000 |
60400 |
680 |
10.4 |
26.0 |
| Uranus |
14500 |
23600 |
1600 |
10.4 |
26.0 |
| Neptune |
16700 |
22300 |
1650 |
13.8 |
33.6 |
You should be able to see from the
table that this gravitational field at the surface of a planet does not just depend on the mass
of the planet. For example, if you look at the gravitational field at the surface of Saturn it is
the same as that on the surface of Uranus although Saturn is much more massive.
The size of this gravitational field is very important – if it too large we would be
pulled so strongly to the surface that we would be crushed. For this reason creatures that
lived on planets with high gravitational fields (high g) would need strong skeletons and really
thick legs!
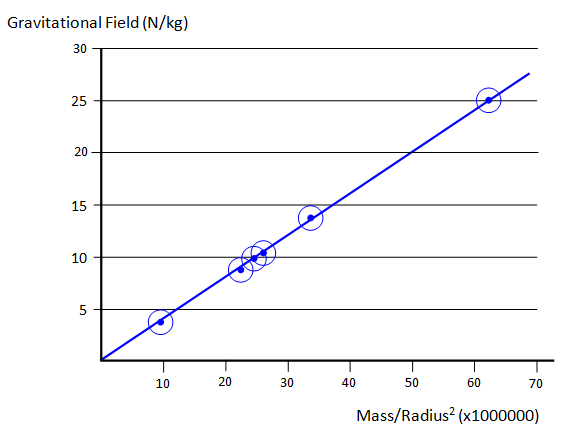
The graph
shows the way in which mass and radius affect the size of the gravitational field.
The
following graph gives you a way of working out the gravitational field on any planet, or other
astronomical body such as one of the moons in the solar system, if you know its mass and its
radius.
Pluto (a minor planet orbiting the Sun usually outside the orbit of Neptune)
has a mass of 2.1 (compared with the Earth at 1000) and a mean radius of 1195 km. From a
detailed version of the graph the graph the value of g on the surface of Pluto would be 0.58
N/kg.
Another way of finding the value of g is to
use the radius of the planet and its density.

Use the data four the first four planets in
the table to plot a graph of the surface gravitational field (g) against the (density x
radius)/1000000.
Use your graph to work out the surface gravitational field on the
following moons of the Solar System.
| Moon |
Radius (km) |
Density
(kg/m3 |
| Io (a moon of Jupiter) |
1830 |
3550 |
| Ganymede (a moon of Jupiter) |
2634 |
1940 |
| Callisto (a moon of Jupiter) |
2403 |
1860 |
| Titan (a moon of Saturn) |
2576 |
1880 |
| Titania (a moon of Uranus) |
789 |
1600 |
| Triton (a moon of Neptune) |
1352 |
2070 |
(Photographs: courtesy of NASA)
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB