
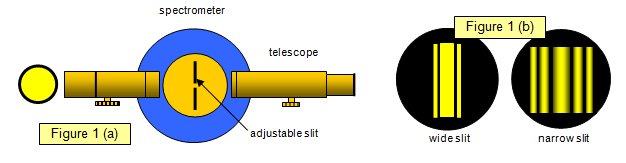
The Fraunhofer diffraction due to a single slit is very easy to observe. An adjustable slit is placed on the table of a spectroscope and a monochromatic light source is viewed through it using the spectroscope telescope (see Figure 1(a)). An image of the slit is seen as shown in Figure 1(b). As the slit is narrowed a broad diffraction pattern spreads out either side of the slit, only disappearing when the width of the slit is equal to or less than one wavelength of the light used.
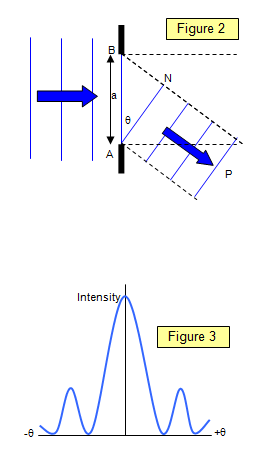
The diffraction at a single slit of width a is shown in Figure 2.
Diffraction occurs in all directions to the right of the slit but we will just concentrate on one
direction towards a point P in a direction θ to the original direction of the waves. Plane waves
arrive at P due to diffraction at the slit AB. Waves coming from the two sides of the slit have a
path difference BN and therefore interference results.
But BN = a sin(θ), and if this is
equal to the wavelength of the light (λ) the light from the top of the slit and the bottom of the slit
a will cancel out.and a minimum is observed at P. This is because if the path difference between
the two extremes of the slit is exactly one wavelength there will be points in the upper and lower
halves of the slit that will be half a wavelength out of phase.
Therefore the general
condition for a minimum for a single slit is:
The path difference between light
from the top and bottom of the slit is written mλ where m is the number of wavelengths 'fitting
into' BN. m is also known as the 'order' of the diffraction image.
If the intensity
distribution for a single slit is plotted against distance from the slit, a graph similar to that shown
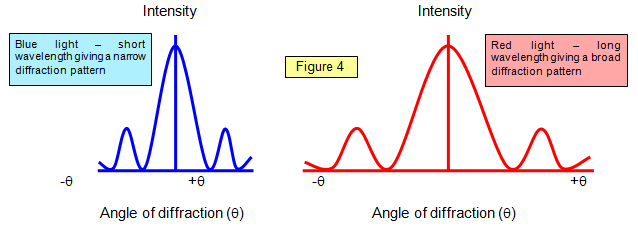
that shown in Figure 3 will be obtained. The effect on the pattern of a change of wavelength is
shown in Figure 4.