Mean free path of molecules in a gas

The molecules in a gas are assumed to be in continuous random motion making collisions with each other and with the walls of the container. The mean distance that the molecules travel between one collision and the next is called the mean free path of the molecules.

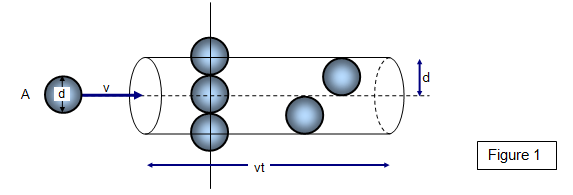
Consider a molecule A with an effective diameter d travelling with a velocity v (see Figure 1). In a time t the molecule will travel a distance vt and collide with π d²vtn molecules, where n is the number of molecules per unit volume (Figure 1). The molecule collides with all molecules whose centres are within a cylinder of length vt and cross-sectional area πd²

The mean free path is the total distance covered (vt) divided by the number of collisions. Therefore the mean free path us given by:

Mean free path (L) = vt/[πd²nvt] = 1/[πnd²]

This proof assumes that all the other molecules remain at rest. If we consider the case of moving molecules the formula must be modified and becomes:

Mean free path (L) = = 1/√2[πnd²]

For air at 0^oC and at a pressure of 1 atmosphere d = 2x10^-10 m and n = 3 x 10²⁵ m^-3. This gives a mean free path for air molecules in these conditions of 2x10^-7 m or 200 nm, about a thousand molecular diameters. Each molecule makes about five thousand million collisions per second!

At an altitude of 100 km the mean free path is 1 metre and at 300 km it is nearly 10 km.

At a depth of 5 000 m in a mine the density of air has risen to 2.32 kg m^-3 and the mean free path is then reduced to about 75 nm.

A further practical study of the mean free path in a gas may be made with the bromine diffusion experiment. In this experiment bromine vapour is allowed to diffuse through air at atmospheric pressure in a closed tube. The average distance d that the bromine diffuses in a certain time t is found by measuring the progress of the 'middle brown' colour of the bromine gas.

DANGER - ONLY TO BE PERFORMED IN A FUME CUPBOARD BY A QUALIFIED TEACHER

Now it can be shown statistically that d is related to the mean free path (L) of the gas by the formula:
d = L[N]^1/2
where N is the number of collisions made while the bromine is diffusing through the distance d.

However, the total distance travelled by an indi vidual molecule of bromine is D, where D = NL, and therefore:

Mean free path (L) = d²/D

Using the kinetic theory formula the velocity of the gas molecules may be found and hence the total distance D travelled in a certain time T. The mean free path can then be found.

Example problems
Using the data in the text calculate the number of air molecules per cubic metre (n) at the following places in the atmosphere.
(a) a height of 100 km
(b) a height of 300 km
(c) a depth of 5000 m in a mine.

Use: n = 1/√2[πLd²]

(a) n = 5.627x10¹⁸/1 = 5.6x10¹⁸
(b) n = 5.627x10¹⁸/10⁴ = 5.6x10¹⁴
(c) n = 5.627x10¹⁸/75x10^-9 = 7.5x10²⁵