A thought experiment on time dilation

Imagine a person in a train with a torch (Figure 1). They shine the beam of the torch across the carriage and time how long it takes to return to them. Very simply it is just the distance the light travels (twice the width of the carriage (d)) divided by the speed of light (c). Someone on the embankment by the train will also agree with the measurement of the time that the light beam takes to get back to the person with the torch after reflecting from the mirror.
They will both say that the time (t) is 2d/c.

Now consider what happens as the train moves at a constant speed along the track.
The person in the train still considers that the light has gone from the torch, straight across the carriage and returned to them. It has still travelled a distance of 2d and if the speed of light is c the time (t) it has taken is 2d/c.

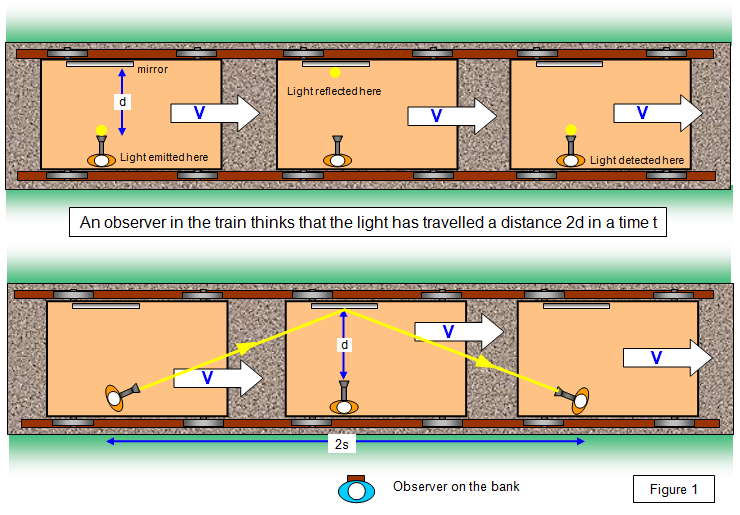
However to the person on the embankment this is not the case. They will observe the light beam moving a distance given by the equation:

Distance travelled by light according to an observer on the bank = 2[d² +s²]^1/2
because the train has moved along a distance s while the light beam crosses the train and returns to the observer.
Now in classical physics, pre relativity, we would now say that since the light beam has moved further in the same time it must be moving faster, in other words we have to "add" the speed of the train to the speed of the light.

But the theory of relativity does not allow us to do this. It says that the speed of light is constant. So we must alter something else. The "something else" is the time, we have to assume that the light has had longer to travel the greater distance – in other words more time has passed for the observer on the bank than for the observer in the carriage. This is called time dilation.
We will call the time for the "stationary" observer on the embankment to.

We can prove just how much longer by the following piece of algebra.
If the train moves at a speed v we have:
Time taken (t_o) = 2s/v = 2 [d² +s²]^1/2/c but t = 2d/c
Therefore: 4[d² + s²]/c² = t_o² and so: 4[c²t²/4 + v²t_o²/4] = c²t_o²
Giving:   c²t² + v²t_o² = c²t_o² and so finally:

The observer on the bank thinks that a longer time interval has passed than the person in the train.

We define a quantity called the relativistic factor (γ) as 1/[1 – v²/c²]^1/2 Such that:


Note that γ is greater than 1.