Quantised orbits

The simple Rutherford model of the atom had one serious disadvantage concerning the stability of the orbits. Bohr showed that in such a model the electrons would spiral into the nucleus in about 10^-10s, due to electrostatic attraction. He therefore proposed that the angular momentum of the electron should be quantised, in line with Planck's quantum theory of radiation.

He stated that the allowed values of the angular momentum would be integral multiples of h/2π, that is:

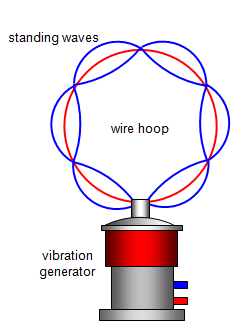
This implied a series of discrete orbits for the electron. We can imagine the electron as existing as a wave that fits round a given orbit an integral number of times.

In other words, if r is the orbit radius and λ the wavelength:

A very simple analogy of this is shown in the diagram above. If we fit a circle of copper wire to a vibrator and then oscillate it series of resonance positions can be found where an integral number of waves fit round the orbit.

Verification of Bohr's principle

The idea of the electron's discrete or quantised orbits within an atom can now be verified. We have two proposals:
(a) that of Schroedinger, suggesting that n electron waves can be fitted around an orbit, that is: 2πr = nλ
(b) that of de Broglie, who proposed that electrons have a wavelength: λ = h/mv

Therefore: 2pr = nh/mv and so mvr = nh/2π

But the quantity mvr is the angular momentum of the electron, and therefore Bohr's original proposal had been confirmed, since n is an integer. (As we have seen, the quantity h/2π is usually written as h bar.

Within a few years of 1923 the wave hypothesis was developed into the theory known as Wave mechanics, by Schroedinger and others.

Each electron also possesses an internal angular momentum called spin, which must be conserved in nuclear and atomic processes. Spin gives rise to a magnetic moment of the electron within the atom.