Einstein's equation and the potential well

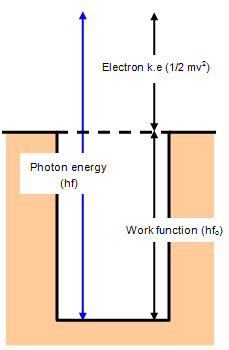
If a quantum of radiation with an energy greater than the work function E_o, and therefore a frequency greater than f_o, falls on a surface an electron will be emitted with some kinetic energy and escape from the surface.

The kinetic energy of the electron is then just the difference between the energy of the quantum and the work function of the metal.
This can be expressed in the following equation - called Einstein's photoelectric equation.

This is shown in the diagram.

If we put a collecting electrode in front of the emitting surface in a vacuum we can detect the photoelectrons as a small current. Changing the frequency of the radiation will not have any effect on the current as long as it is bigger than f_o but increasing the intensity will increase the current.
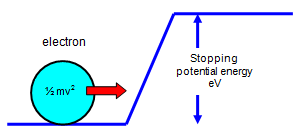
Now if we make the collecting electrode slightly negative compared with the emitting surface the electrons will find it difficult to get to it and electrons will only do that if their energy is greater than the "height" of the potential barrier.

They will be detected if ½ mv² > eV

where V is the potential difference between the emitting surface and the collecting electrode.

Therefore Einstein's equation can be written as:



If V is increased so that no more electrons can reach the detector this value for the potential is called the stopping potential for that surface and radiation.