REFRACTION

For a simple introduction to refraction look at the Refraction file in the 11-14 section.
(See: 11-14/Light/Text/Refraction)

When light waves pass from air into a more dense material such as water, glass, plastic etc. they slow down. The ratio of their velocity in air (or more correctly in free space) to their velocity in the material is called its refractive index.


The table below shows the refractive indices of some common substances. One of the reasons why diamonds sparkle is partly connected with their high refractive index (their shape also has something to do with it!)

Material	Refractive index		Material	Refractive index
Diamond	2.42		Glycerol	1.47
Ruby	1.76		Magnesium fluoride	1.38
Duodomethane	1.74		Water	1.33
Carbon disulphide	1.63		Ice	1.31
Glass (flint)	1.53-1.96		Air at STP	1.000 298
Glass (crown)	1.48-1.61

Note the magnesium fluoride – this is used in non-reflecting coatings, blooming of lenses).

The change of velocity when light moves from one medium to another gives a change of direction when the beam hits the boundary at an angle. When the light travels from a less dense material such as air into more dense material such as glass it bends towards the normal, bending away from the normal when its direction is reversed.


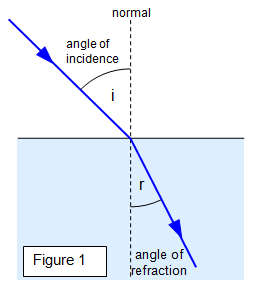
The law relating the angle of incidence (i), the angle of refraction (r) and the refractive index (n) was discovered in 1621 by Willebrod Snell and is therefore known as Snell's Law.

Snell's law states that:

The absolute refractive index of a material is that compared to free space which is given a refractive index of 1.000.

For light passing from one medium of absolute refractive index n₁ to another of absolute refractive index n₂ the refractive index of the interface is written as ₁n₂.

The refractive index of the material also depends on the wavelength of the radiation being considered. This relation is given by Cauchy's theorem:

The refractive index of two different types of glass for three different wavelengths is given in the following table.

	nC	nD	nF
Crown glass	1.5150	1.5175	1.5233
Flint glass	1.6434	1.6550	1.6648

n_C is the refractive index for the C line of hydrogen wavelength 656 nm
nD is the refractive index for the F line of hydrogen wavelength 589 nm
nF is the refractive index for the F line of hydrogen wavelength 486 nm

(See also: 16-19/Optics/Refraction/Text/Achromatic prisms and lenses)

Light passing from one transparent material to another

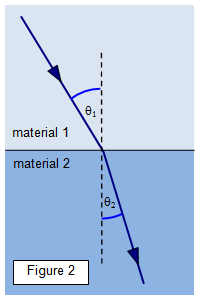
Consider a beam of light passing from material 1 to material 2. (Figure 2) Let the absolute refractive indices of the materials be n₁ and n₂ respectively.
We have:

If the direction of the light is reversed:




Therefore: ₂n₁ = 1/[₁n₂]

Notice that we have made an important assumption here, namely that the light will follow the same path whether it is travelling in one direction or the other. This is known as the principle of reversibility of light.

If the refractive index for light going from air to glass is 1.5 then if the light is traveling from glass to air the refractive index would be 1/1.5 = 0.67

Velocity considerations

When light passes from one transparent material to another of different refractive index its speed changes. The ratio of the speeds in the two materials is the inverse ratio of the refractive indices of the two materials

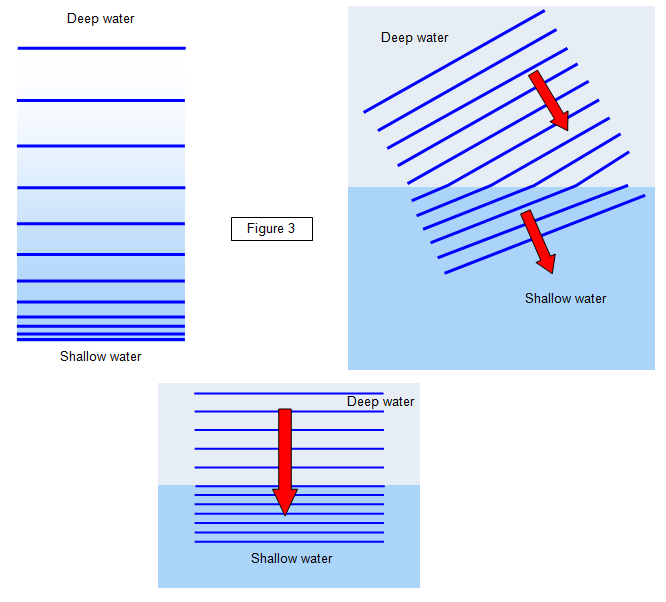
Wave refraction

The top left hand diagram shows the effect on the waves due to a sloping beach and the other two diagrams show the result of a sudden depth change.