Refraction through right angled prisms

We will consider first the refraction of monochromatic light through right angled prisms. The effect of different wavelengths is considered elsewhere.

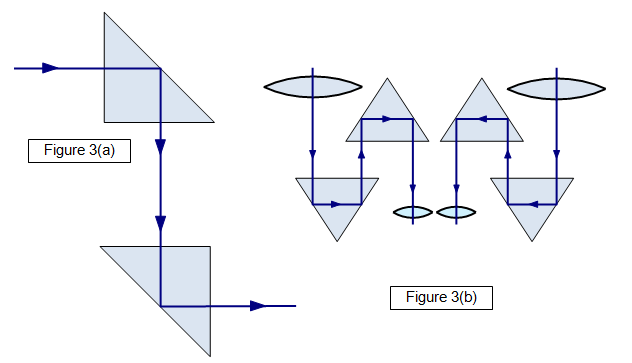
Firstly right angled prisms. Since the critical angle for a glass-air boundary is 42^o any light which hits the boundary at 45^o will be totally internally reflected. This explains the following three diagrams (Figures 1, 2 and 3).



Figure 3(a) shows how right- angled prisms are used in a periscope, and Figure 3(b) shows their use in prismatic binoculars.

Refraction through prisms of angles other than a right angle

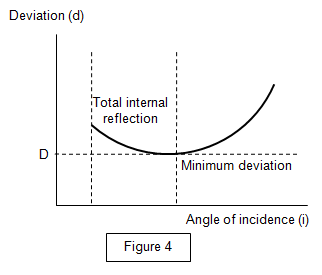
We will now consider the refraction of monochromatic light through prisms with refracting angles other than a right angle. When light passes through a prism it is deviated, and the angle of deviation d depends upon the angle of incidence i of the light on the first face of the prism. If d is plotted against i then a graph like that in Figure 4 will be obtained. You will notice that there is a minimum deviation (D) for a certain value of incidence.

By the principle of reversibility it should be clear that this point of minimum deviation occurs when the light passes symmetrically through the prism.

This minimum deviation can be used to find the refractive index of the material of the prism. If a hollow glass prism filled with liquid is used, the refractive index of the liquid can be measured. The theory is shown below.

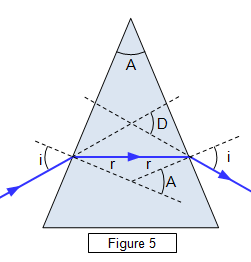
Let the angle of minimum deviation be D and the refracting angle of the prism be A.

Therefore from Figure 5 A = 2r and n = sin i/sin r

and so D - (i - r) + (i - r) = 2i - 2r

Therefore: i = (D + A)/2 and

schoolphysics monochromatic refraction through prisms animation

To see an animation of the refraction of monochromatic light through a prism click on the animation link.

schoolphysics refraction of light of different colours through prisms animation

To see an animation of the refraction of light of different colours through prisms click on the animation link.

Refraction through prisms of small angle

Consider now a small-angled prism as shown in Figure 6.

The deviation (d) = (i - r) + (i' - r') and the refracting angle (A) = r + r'.

If the refracting angle of the prism is small then i, i', r and r' are also small and so:
i = nr and i' = nr'

Therefore:

d = nr + nr' - A
= n(r + r') -A
= nA - A
= (n - 1)A


The deviation for a prism of small angle is therefore given by: