Formula for a thin lens

Using the real is positive - virtual is negative sign convention the formula for a thin lens can be shown to be:

This applies to all types of lens as long as the correct sign convention is used when substituting values for the distances.
(Reminder: we use the 'real is positive, virtual is negative' sign convention.)

For a treatment using waves and the curvature of the lens surface see Lenses and waves)

Two proofs of the formula will be given here, one a geometrical proof and the other an optical version.

(a) Geometrical proof of the lens formula

Consider a plano-convex lens, as shown in Figure 1.


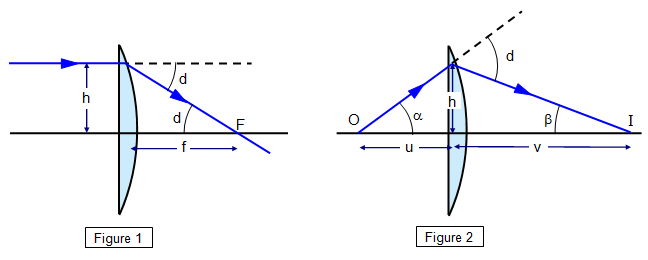
If we consider the action of the lens to be like that of a small-angle prism, then all rays have the same deviation. Therefore, in Figure 2,

Deviation (d) = α + β and so for small angles tan d = tan α + tan β

Therefore: h/f = h/u + h/v and so 1/f = 1/u + 1/v and the formula is proved.

(b) Optical proof of the lens formula

We will only consider the case for a biconvex lens here. (see Figure 3).


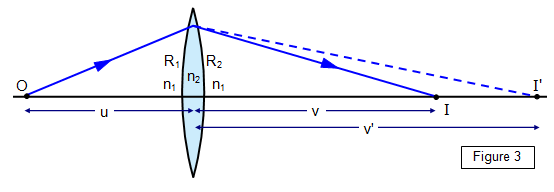
Consider the two spherical surfaces of the lens. For the first surface we have

n₂/v' + n₁/u = [n₂ – n₁]/R₁

For the second surface we have

n₂/-v' + n₁/v = [n₂ – n₁]/R₂

(note the negative sign denoting a virtual object for the second surface).

Combining these two equations gives:


If n₁ = 1 (i.e. the lens is in air) the formula becomes:

1/u + 1/v = 1/f

This formula could be used to calculate the refractive index (n₂) of the glass of the lens.