Vectors in equilibrium – general principles

For an object to be in equilibrium it must not have a tendency to:
(a) translate – i.e. move from one place to another
(b) rotate – i.e. turn

In order to satisfy these conditions the following must apply:

ONE FORCE

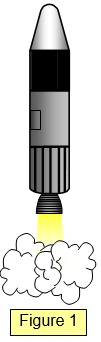
If there is only one force acting on the body it cannot be in equilibrium. It may not rotate (if the force passes through the object's centre of mass) but it is bound to move. (See Figure 1 for a rocket in deep space).

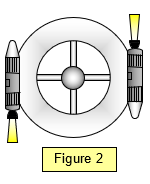
TWO FORCES

If two forces act on the body it can only be in equilibrium if the two forces are equal and opposite and lie in the same line. If they are equal and opposite but not in the same line they form a couple and the object will rotate. (See the space station in Figure 2)



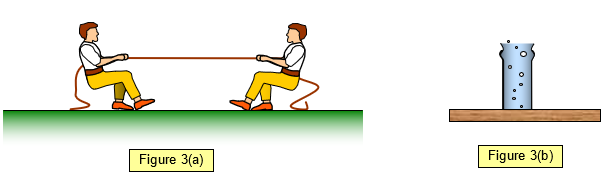
If they are in the same line as well as being equal and opposite then the object will be in equilibrium (See the tug of war or a glass on a table in Figures 3(a) and (b)).

schoolphysics: Vectors and a rope

To see an animation of the effect of the direction of forces on equilibrium click on the animation link.

THREE FORCES

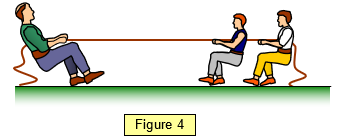
If three forces act on a body it can be in equilibrium if they are parallel or not and in the same line or not.

The simplest case is where the sum of the two forces acting in one direction is equal to the third force acting in the opposite direction (Figure 4).



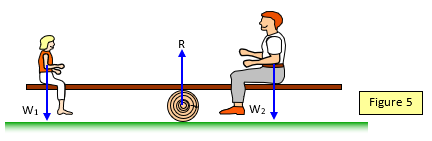
A case where the three forces are in parallel but not acting through the same point is shown by the see saw in Figure 5. The resultant moment must be zero. Notice that the downward forces (the weights of the two people) are balanced by an upward force (R) at the pivot.

Non-parallel forces

Finally we must consider the case of three forces that are not in parallel.

From the first condition for equilibrium it follows that if three non-parallel forces act on an object that is in equilibrium then the lines of action of these three forces must pass through one point.

If this were not true then taking moments about the point (P) where two of the forces cross (i.e. their total moment is zero) would still leave a resultant moment due to the third force.(See Figure 6).


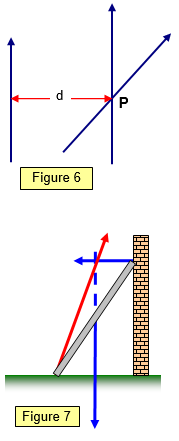
A simple example of three forces meeting at a point and giving equilibrium is a ladder leaning against a wall. (See Figure 7).



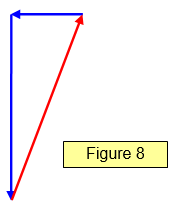
The vectors (in this case the forces) can be represented in magnitude and direction by the three sides of a triangle – the vectors must be drawn so that their direction follows round the figure. See the example set of forces for the ladder shown in Figure 8.