The simple pendulum
Consider a pendulum of length L with a mass m at the
end displaced through an angle θ from the vertical (Figure 1). The restoring force F is the
component of the weight of the bob. Therefore
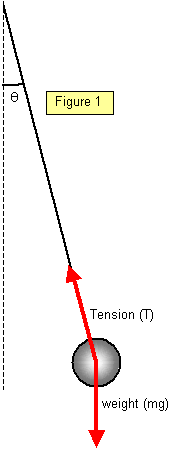
F = - mg sinθ = ma giving a = - g sinθ
But for small angles sin θ tends to
θ
c, and therefore a = -gθ = - gx/L
where
x is the distance of the bob from the midpoint of the oscillation. The acceleration is
proportional to the negative of the displacement and so the pendulum therefore moves with
simple harmonic motion.
The value of ω
2 is g/L, and so the period of a
simple pendulum is
Period of a simple pendulum (T) = 2π[L/g]1/2
(this formula
is only accurate for small angles of swing, however).
An alternative treatment uses
the idea of the moment of inertia of the bob (mL
2) and the restoring couple (C = - mg
sinθ L).
Since C = Iα we
have: - mg sin θL = Iα =
mL
2α
Therefore the angular acceleration (α) = -
gθ/L for small θ giving the same
result as the first proof.
Example problem
Calculate the length of a simple pendulum that will have a period of exactly one second. (g = 9.81 ms-2)
L = [T2g]/4π2 = [1x9.81] /39.47 = 0.25m
The measurement of the
acceleration due to gravity
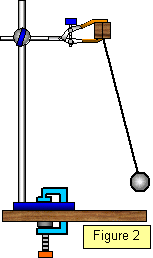
A
simple pendulum may be used to measure the acceleration due to gravity (g). The period is
measured for a series of different values of L and a graph plotted of T
2 against L.
The gradient of this graph is L/T
2 and this is equal to
g/4π
2.
Therefore g = 4π
2L/T
2 From this the
value of g can be found. Very accurate determinations by this method have been used in
geophysical prospecting.
Simple pendulum with large angles of
swing
For large angles of swing (θ) the period of the simple
pendulum is:
T = 2π[L/g(1+[1/2
2]sin
2θ +
[1.3
2/2
2.4
2]sin
4θ+...)]
1/2
although the simple formula is accurate to ±0.5 per cent for θ<15%.
A
simple pendulum of length 1 m has a theoretical period of swing (using the simple formula) of
2.006 s. If the swing is now increased to 45
o this becomes 2.131
s.
Student investigation
Use a pendulum at least 2 m long with a small but heavy bob to make a determination of the acceleration due to gravity. Include in your results an estimate of the accuracy, taking into account the angle of swing if you consider it to be an important factor.
