Stability of rotating objects
Since angular momentum is a vector
quantity a couple is needed to change the angular momentum of a body. It therefore
follows that spinning objects are more stable than ones that do not spin. For this reason a
spin pass in rugby is more likely to go straight, rifle barrels are grooved (rifled) to make the
bullets spin in flight and satellites are given a spin when they are launched from the space
shuttle.

Example problem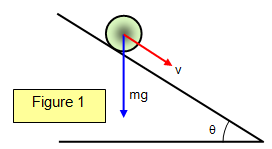
Figure 1 shows an object rolling down a hill.
Such an object will gain rotational as well as
translational kinetic energy as it loses potential
energy.
Show that the acceleration of a rolling cylinder
is less than that of one that slides down a slope
without rolling providing there is no friction.
Loss of potential energy = mgh = gain in kinetic energy
= 1/2 mv
2 + 1/2 Iω
2 = 1/2 mv
2+ 1/2 I(v
2/r
2)
For a cylinder of mass m rolling down a slope of angle θ the kinetic energy is:
ke.= 3/4 mv
2 (since the moment of inertia of a solid cylinder = mr
2/2)
The loss of potential energy is mgs sin θ where s is the distance travelled down the slope.
Therefore mgs sin θ = 3/4 mv
2 and this gives the acceleration as 2/3 gsin θ.



