Newton's Third law

This law concerns the equal and opposite forces that act between two bodies. The forces may be the same but the results in collisions may be very different - think about the effects on a stone wall and on your fist if your are silly enough to punch the wall. When a bullet leaves a gun there is a force on the bullet but there is also and equal and opposite force on the gun that makes it recoil.

Newton's Third law can be stated as:

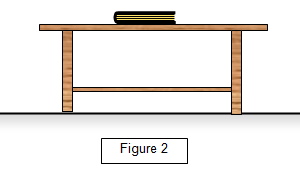
You can demonstrate this accurately by fixing two spring loaded trucks together on a linear air track. When the spring is released they both move off - showing that there is a force on both. The acceleration of each truck depends on its mass and this could be checked using two light gates. If the masses of the trucks are equal they will accelerate at the same rate whereas trucks of different masses will have different accelerations (Figure 1).

Another way is to use a spring balance and a compression balance fixed together. Pushing down on the compression balance will stretch the spring balance - the change in both readings should be the same.

The Newton Pair

It is important to remember that the forces mentioned in Newton's Third Law are of a certain 'type'. The two forces are known as a 'Newton pair'.

A Newton pair of forces has the following properties:

(a) These two forces act on two different bodies.
(b) Both forces are always of the same type (i.e. both gravitational, both electrostatic, etc.).
(c) The forces are equal in magnitude.
(d) The forces act in opposite directions.

A book on a table can be used to explain the idea of a Newton Pair. (See Figure 2)
In this example there are two Newton pairs.
(a) Gravitational forces - the pull of the Earth on the book and the pull of the book on the Earth
(b) Contact forces - the push of the book on the table and the push of the table on the book
You should notice that in each case if one of the forces of the pair is removed it makes the other one vanish.

A car and a caravan

Let's think about a car towing a caravan. The force of the tow bar on the caravan is the same as the force of the tow bar on the car - if this were not true the car would either accelerate faster than the caravan - stretching the tow bar and leaving the caravan behind or the caravan would accelerate faster than the car and start overtaking it! So you see there are two equal and opposite forces but each one acts on a different object - one on the car and one on the caravan and both the car and caravan can still move forwards. The forces are a Newton pair – both being contact forces.

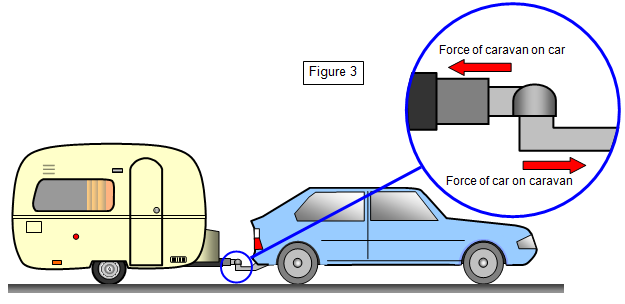
But how do they accelerate? To understand this we have to look at the forces between the driving wheels of the car and the road. Here again there are two equal and opposite forces one of the road on the car and the other the car on the road. Since the road stays still the car accelerates forward taking the caravan with it. The acceleration of the car and caravan is the thrust of the car engine (minus any drag) divided by the total mass of car and caravan.

(See: Car towing a caravan for a numerical example)

The monkey and the bananas

A fascinating problem! A weightless rope hangs over a frictionless pulley. (Yes I know it's unlikely but it makes the problem simpler!). On one end of the rope is a monkey with a mass of 25 kg and on the other a bunch of bananas also with a mass of exactly 25 kg hanging a metre or so above the monkey.

The monkey wants to eat the bananas and so starts to climb the rope - what happens to the distance between the monkey and the bananas?

It stays the same - equal and opposite forces act on the monkey and the bananas and since they have the same mass they both accelerate and at the same rate - the distance between them therefore doesn't alter.